Метод полной взаимозаменяемости.

Такое решение р.ц. когда детали включены в цепь, в качестве звеньев, без выбора или пригонки обеспечивают заданную точность замыкающего звена.

Обратная задача – сущность метода заключается в том, что расчет размера замыкающего звена ведется в предположении, что звенья цепи имеют предельные размеры (максимальные, минимальные) и находятся в нанеивыгоднейшем сочетании. Этот метод наз. расчет на max и min.

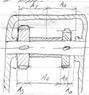
Подставим номинальные размеры в уравнение (1):

Ao=A1+A2-A3-A4-A5

Найдем предельное значение замыкающего звена.

┌Aomax=A1max+A2max-A3min-A4min-A5min

└Aomin=A1min+A2min-A3max-A4max-A5max

TAo=TA1+TA2+TA3+TA4+TA5

TAo=Σ(i=1;n)TAi [2]

n – кол-во составляющих звеньев.

Найдем верхнее и нижнее отклонение замыкающего звена:

EsAo=Aomax-Ao

┌Aomax=A1max+A2max-A3min-A4min-A5min

└Ao=A1+A2-A3-A4-A5

EsAo=EsA1+EsA2-EiA3-EiA4-EiA5

EsAo=Σ(i=1;m)EsAi^ув. – Σ(j=1;p)EiAj^ум. [3]

EiAo=Aomin-Ao

Аналогично:

EiAo=Σ(i=1;m)EiAi^ув. – Σ(j=1;p)EsAj^ум. [4]

Введем понятия координаты середины поля допуска звена (по другому- среднее отклонение).

Решаем обратную задачу методом max-min:

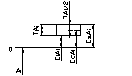
┌EsAi=EcAi+TAi/2 [5]

└EiAi=EcAi-TAi/2

Подставим (5) в (3)-(4), получим (6):

EcAo=ΣEcAi^ув. – ΣeiAi^ум. [6]

Дата добавления: 2015-07-10