Расчёт долговечности силовых элементов

3.1. Последовательность расчёта долговечности

Результаты расчёта силовой конструкции на статическую прочность позволяют на этапе проектирования оценить долговечность её элементов.

Оценка циклической долговечности конструкции, спроектированной на безопасный ресурс, т.е. на эксплуатацию до появления видимых трещин, включает следующие этапы (рис. 21):

- определение в конструкции критических зон;

- формирование блоков нагружения;

- построение кривых усталости;

- расчет долговечности конструкции.

Рис. 21– Блок-схема оценки долговечности

Рассмотрим более подробно элементы блок-схемы, изображённой на рис. 21.

3.2. Определение критических зон конструкции и коэффициентов концентрации

Опасное накопление повреждений происходит в местах с наиболее интенсивным НДС. Эти так называемые критические зоны выделяются еще на этапе проектирования, а затем исследуются экспериментально или расчетным путем.

В приведённой ниже методике расчёта долговечности принимается, что истинное НДС в критических зонах является упругим. В таком случае теоретический коэффициент концентрации напряжений определяем следующим образом [3]:

,

где - эквивалентное максимальное локальное напряжение;

- эквивалентное напряжение в неповрежденном сечении.

Теоретические коэффициенты концентрации напряжений определяются по справочникам, а также расчётным или экспериментальным путём. В дальнейшем экспериментальное определение значения 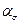рассматриваться не будет.

При расчётном определении теоретического коэффициента концентрации напряжений наиболее часто используют результаты расчёта МНДС исследуемой критической зоны, полученные с применением метода конечного элемента. Максимальное эквивалентное значение локального напряжения определяют непосредственно по эпюре распределения эквивалентных напряжений, примеры которых приведены в п.2.4. Эквивалентное напряжение в неповреждённом сечении определяется двумя способами: по эпюре распределения эквивалентных напряжений на удалении от концентратора (в области, где поле напряжений становится однородным) или из расчёта эквивалентного напряжения по формулам сопротивления материалов (см. п.2.3). Например, для критических зон, приведённых на рис. 16 и 17, были получены теоретические коэффициенты концентрации напряжений и 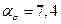, соответственно.

Примеры определения теоретических коэффициентов концентрации напряжений с использованием справочных материалов изложены ниже. При этом определение критических зон производилось по данным статического расчета конструкции АПУ с учетом концентрации напряжений у вырезов. Эти зоны представлены на рис. 22 - 30.

Для плоского напряженного состояния, в рамках которого рассматриваем все концентраторы, эквивалентное напряжение в неповреждённом сечении определяем следующим образом:

,

где - нормальные и касательное напряжения по осям X и Z соответственно.

Коэффициент концентрации в зоне 1. В поле напряжений (рис. 22), вследствие большого относительного расстояния между горизонтальными рядами отверстий, будем эти ряды считать изолированными друг от друга. В пределах каждого ряда в силу тех же причин будем пренебрегать взаимным влиянием НДС, вызванного наличием малых отверстий. Таким образом, имеем комбинированный концентратор напряжений, изображенный на рис. 22. Для полосы конечной ширины с подобным концентратором коэффициент концентрации напряжений равен [3] .

Рис. 22 – Отверстия под фиксирующие штифты

Коэффициент концентрации в зоне 2. Пренебрегая разгружающим влиянием малых отверстий (рис. 23), коэффициент концентрации напряжений определяем для случая изолированного круглого отверстия в полосе конечной ширины следующим образом [4]:

,

где 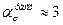- коэффициент концентрации напряжений для изолированного отверстия при однородном растяжении;

- однородное растягивающее напряжение;

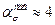- коэффициент концентрации напряжений для изолированного отверстия при чистом сдвиге;

- касательное напряжение.

Рис. 23 – Резьбовые отверстия под крепеж

Подставляя численные значения из табл. на рис. 23, по приведенной выше формуле получим .

Коэффициент концентрации в зоне 3. Для этой зоны (рис. 24) коэффициент концентрации напряжений равен [3] .

Рис. 24 – Технологический лючок и отверстия

Коэффициент концентрации в зоне 4. Вид нагружения в указанной зоне представлен на рис. 25. В соответствие с формулой, представленной ранее, получаем значение коэффициента концентрации напряжений .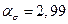

Рис. 25 – Отверстия под крепеж баллона (зона 4)

Коэффициент концентрации в зоне 5. Вид нагружения в указанной зоне представлен на рис. 26. В соответствии с [3, 4] и формулой для расчета 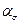вычисляем коэффициент концентрации напряжений: .

Рис. 26 – Технологический лючок с отверстиями под крепеж

крышки (зона 5)

Коэффициент концентрации в зоне 6. Вид нагружения этой зоны представлен на рис. 27. Пренебрегая разгружающим влиянием малых отверстий, будем рассматривать концентратор как узкий прямоугольный вырез с закругленными краями в бесконечной пластине.

Рис. 27 – Лючок и отверстия под крепеж электроразъема

В соответствии с [3, 4] и формулой для расчета 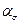вычисляем значение коэффициента концентрации напряжений: .

Особенности НДС зоны 7. Участки с наиболее интенсивным НДС этой зоны заштрихованы на рис. 28. Там же представлены соответствующие поля напряжений.

Рис. 28 – Передний пилон подвески АПУ (зона 7)

Локальные возмущения НДС в этой зоне имеют место в узлах подвески (рис. 29 и 30), оценка прочности которых произведена в предыдущем разделе.

Рис. 29 – Узел подвески переднего пилона

Рис. 30 – Узел подвески заднего пилона

3.3. Блоки нагружения

Современные достижения в оценке циклической долговечности развиваются в двух направлениях:

- с непосредственным использованием случайного спектра эксплуатационных нагрузок;

- со схематизацией реального спектра нагрузок.

Мы используем второе направление. Процесс нагружения представляется в виде последовательности блоков отнулевых циклов различной интенсивности и знака. При этом влиянием частоты пренебрегаем и считаем, что нагружение конструкции - повторно-статическое.

Схематизация методом полных циклов предполагаемого случайного процесса изменения нагрузки в процессе эксплуатации АПУ позволила получить повторяемость нагрузок на один лётный час (рис. 31), содержащую только пульсирующую нагрузку.

Рис. 31 – Блок нагружения

3.4. Построение кривых усталости

Основной трудностью при оценке циклической долговечности на этапе проектирования и при последующей отработке конструкции является получение кривых усталости для всех критических зон. Поэтому в настоящее время делаются попытки упрощенного аналитического построения этих кривых [5]. Во всех случаях при этих построениях предполагаются известными:

- физико-механические характеристики материала;

- закон, связывающий амплитуду и долговечность в диапазоне 10³ – 10⁶ циклов;

- значение коэффициента снижения предела выносливости для материала критической зоны.

Физико-механическими характеристиками, необходимыми для построения кривой усталости критических зон, являются предел выносливости материала при заданном коэффициенте асимметрии цикла напряжений ; предел прочности материала ; предел текучести материала 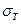(допускается использовать условный предел текучести ) и показатель наклона кривой усталости .

Приведённые физико-механические характеристики являются справочными. Причём в справочниках по характеристикам усталости конструкционных материалов наиболее часто задаётся предел выносливости при симметричном цикле изменения напряжений, т.е. при .

В случае отсутствия данных по пределу выносливости материала при симметричном цикле изменения напряжений значение допускается приближённо определять по следующей зависимости:

при .

Так как полученный в предыдущем пункте блок нагружения содержит только пульсирующую нагрузку, то реализуемое изменение напряжений в критической зоне будет тоже пульсирующим или отнулевым с коэффициентом асимметрии 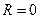. В этом случае необходимо привести значение к значению предела выносливости при отнулевом цикле изменения напряжений. Приведение к 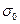осуществляется по формуле Одинга:

,

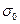где и - амплитуда симметричного и заданного (пульсирующего) циклов соответственно;

R - коэффициент асимметрии исходного (симметричного) цикла;

- константа, являющаяся характеристикой материала, варьируется в диапазоне от 0,4 до 0,6 (в случае отсутствия данных по допускается принять =0,5). Для стали BHC-2 = = 0,4696 [7].

Значение показателя наклона кривой усталости также является справочным, в случае отсутствия данного значения допускается использовать следующую формулу [8]:

,

где (σВ в МПа);

- значение коэффициента снижения предела выносливости для материала критической зоны (рассматривается далее).

Помимо асимметрии напряжений, на значение предела выносливости существенно влияют такие факторы, как концентрация напряжений, масштабный фактор, состояние поверхности, шероховатость и т.д. Учёт данных факторов для конкретных критических зон предела выносливости производится по формуле

,

где - предел выносливости материала критической зоны при отнулевом цикле напряжения;

- предел выносливости гладких образцов при пульсирующем цикле;

K - коэффициент снижения предела выносливости,

.

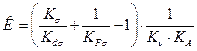Здесь - эффективный коэффициент концентрации напряжений;

- коэффициент влияния абсолютных размеров поперечного сечения;

- коэффициент влияния шероховатости поверхности;

- коэффициент влияния поверхностного упрочнения;

- коэффициент анизотропии.

Эффективный коэффициент концентрации напряжений определяется приближённо по следующей формуле:

,

где 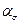- теоретический коэффициент концентрации напряжений;

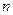- коэффициент.

Значения коэффициента 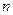обычно варьируются в диапазоне 1,0÷2,0 и зависят от относительного градиента напряжений и предела текучести 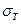. Коэффициент 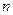определяется по зависимости

,

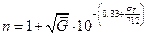где - имеет размерность, ;

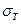- имеет размерность, .

Для определения относительного градиента напряжений можно воспользоваться приближённой формулой

,

где - радиус в месте концентрации напряжений,мм.

Также при определении эффективного коэффициента концентрации напряжений можно воспользоваться зависимостью

,

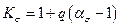где 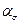- теоретический коэффициент концентрации напряжений;

- коэффициент чувствительности металла к концентрации напряжений, определяемый в соответствии с рис. 32.

Рис. 32 – Определение коэффициент q

Значение коэффициента влияния абсолютных размеров поперечного сечения определяется по формуле

,

где - предел выносливости при растяжении-сжатии.

Для выполнения курсовой работы можно приближённо принять .

Коэффициент , характеризующий снижение предела выносливости за счёт шероховатости поверхности детали, определяют приближённо по формуле

,

где 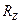- шероховатость, мкм;

- предел прочности материала, МПА.

Коэффициенты влияния поверхностного упрочнения и анизотропии учитывают эффекты повышения предела выносливости за счёт поверхностного упрочнения (закалка токами высокой частоты, химико-термическая обработка, поверхностный наклёп и т.д.) и особенности эксплуатационного нагружения соответственно. При выполнении курсовой работы допускается принять и , т.е. не учитывать эффекты повышения значения предела выносливости.

Вычисленные по данной методике значения величин K, m и для критических зон конструкции АПУ-470 приведены в табл. 5.

Таблица 5

Характеристики кривой усталости

п/п №	Критические зоны	К	, МПа	m
	Зона 1 Зона 2 Зона3 Зона 4 Зона 5 Зона 6	4,48 4,63 9,1 3,75 6,61 5,66	85,5 82,7 42,1 102,1 57,9 67,7	4,53 4,39 2,23 5,42 3,07 3,59

Имея необходимые физико-механические характеристики материала и значение коэффициента снижения предела выносливости критической зоны, можно аналитически описать кривую усталости в диапазоне 10³ – 10⁶ циклов. При этом используется следующая зависимость:

,

где 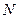- число циклов до появления видимой усталостной трещины или до разрушения при заданном значении напряжения ;

- показатель наклона кривой усталости.

С учётом приведённой зависимости, значения предела выносливости и базы испытаний, можно определить число циклов 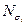до появления видимой усталостной трещины или до разрушения при отнулевом цикле заданного напряжения следующим образом:

,

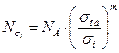где 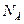- база испытаний, является справочной характеристикой и изменяется от 10⁶ до 10⁷ циклов (в случае отсутствия данных принимается 10⁶ циклов).

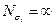Если значение действующего в опасной зоне напряжения не превышает значения , то принимается, что и данное значение не определяется. В таком случае при последующих расчётах считается, что циклы с напряжением не вносят повреждения в конструкцию.

Кривая выносливости должна удовлетворять условию консервативности, т.е. должна быть построена по нижним значениям амплитуд переменного нагружения из всего спектра случайных нагружений, соответствующих данной долговечности.

Обобщая известные данные, для построения кривой усталости стали ВНС-2 используем следующий метод. В качестве исходной строим кривую усталости при изгибе гладких круглых образцов (рис. 33). В соответствии с принципом консервативности в качестве опорных точек выбираем:

- при N = 10º - ;

- при N =N_G = 10⁶ (точка перелома кривой усталости) - .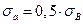

Рис. 33 – Кривые усталости для стали ВНС-2

Как видно из рис. 33, кривые, построенные с использованием этих значений m, лежат выше построенных нами кривых в области N = 10³–10⁶. На этом же рисунке представлена экспериментальная кривая усталости, полученная в работе в аналогичных условиях испытаний. Эта кривая в диапазоне 10³ – 10⁵ также расположена выше кривой, построенной нами.

Таким образом, данная методика удовлетворяет принципу консервативности и пригодна для оценки циклической долговечности конструкций, спроектированных на безопасный ресурс.

3.5. Расчёт циклической долговечности силовых элементов

Расчет циклической долговечности силовых элементов АПУ проводим на основе теории линейного накопления повреждения [9], основное расчетное соотношение которой представим в виде

,

где n_i - заданное в блоке число циклов нагружения при амплитуде ;

N_i - число циклов нагружения до разрушения с той же амплитудой;

K - число ступеней в блоке нагружения;

ξ – мера предельного повреждения.

С учётом коэффициента надёжности η запас по долговечности определяем следующим образом:

.

Значение меры предельного повреждения варьируется от 0,5 до 2 и зависит от последовательности приложения малых и больших нагрузок. Для выполнения работы значение ξ предлагается принимать равным 0,5.

Коэффициент надёжности необходим для обеспечения запаса усталостной прочности исследуемой критической зоны. Его каноническая структура может быть представлена в виде произведения минимального числа сомножителей [17]:

.

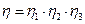Каждый из сомножителей в представленном выше выражении отражает отклонение расчётной оценки важнейших факторов, влияющих на выносливость критической зоны, от их действительных значений.

Величина учитывает ошибки в оценке уровня и характера напряжённости. Она зависит от методов определения напряжённо-деформированного состояния исследуемой критической зоны, наличия точных сведений о нагрузках и т.д. Как отмечалось ранее, при определении местного напряжённо-деформированного состояния критической зоны в большинстве случаев используют метод конечного элемента. Следует отметить, что использование при этом метода вложенных сеток, с помощью которого исследуют сходимость результатов, например напряжений или деформаций в критической зоне, позволяет понизить значение коэффициента .

Величина принимает во внимание отклонения характеристик механических свойств материала от нормативных значений. Она должна быть повышенной для неоднородных материалов (литьё) и крупных деталей, а также деталей сложных форм. И наоборот, например для конструкций, изготавливаемых из листов, при наличии реальной диаграммы деформирования материала коэффициент принимает своё минимальное значение, т.е. становится равным 1,5.

Множитель 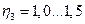учитывает ответственность критической зоны. Это означает, что для критических зон, разрушение которых может привести к отказу всего изделия, данный коэффициент должен иметь значение 1,5.

Результаты расчета циклической долговечности конструкции АПУ по заданному блоку нагружения, построенным кривым усталости и при коэффициенте надежности η = 6,48, приведены в табл. 6.

Таблица 6

Результаты расчета

№ п/п	Критические зоны	σ, МПа	σЭКВ, МПа при РРАСЧ	σЭКВ, МПа при 0,67· РРАСЧ		КДОЛГ
	Зона 1	σХ = -250 τXZ = 0		167,5	0,00034	226,9
	Зона 2	σХ = 96 τXZ = 93	187,5	125,6	0,000092	838,7
	Зона 3	σХ = 0 τXZ = -43	74,5	49,9		∞
	Зона 4	σХ = 18 τXZ = 46	81,7	54,7		∞
	Зона 5	σХ = 96 τXZ = 93	187,5	125,6	0,000433	178,2
	Зона 6	σХ = -22 τXZ = 93	272,7	182,7	0,00796	9,7
	Зона 7 (А)	σХ = 721,3 σZ = 116 τXZ = 100	691,2	463,1		∞
	Зона 7 (Б)	σХ = 330 σZ = 290 τXZ = 310		422,1		∞
	Зона 7 (В)	σХ = 320 σY = 200 τXZ = 290		388,6		∞
	Зона 7 (Г)	σХ = 630 τXZ = 0		422,1		∞
	Зона 7 (Д)	σХ = 680 τXZ = 0		455,6		∞

3.6. Пример расчёта крюка удержания выводных рычагов

Продемонстрируем применение изложенной последовательности оценки долговечности на примере расчёта крюка удержания выводных рычагов, представленного на рис. 18.

Исходными данными для расчёта будет являться результат расчёта МНДС при действии расчётной нагрузки, представленный на рис. 20. Также в качестве исходных данных примем:

- коэффициент безопасности при определении расчётной нагрузки ;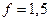

- предел прочности материала ВНЛ-3 МПа;

- условный предел текучести материал ВНЛ-3 МПа;

- предел выносливости при симметричном цикле изменения напряжений материала ВНЛ-3 МПа;

- база определения предела выносливости ;

- качество обработки поверхности крюка (шероховатость) мкм;

- блок нагружения в соответствии с рис. 31.

Критической зоной рассматриваемого крюка будет область наибольших напряжений (определяется из результата расчёта МНДС). Для определения теоретического коэффициента концентрации напряжений 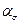произведём расчёт номинальных напряжений, возникающих в одном крюке при заданной расчётной нагрузке F = 5 кН. Для этого составим схему нагружения крюка от заданной нагрузки (рис. 34).

Рис. 34 – Схема нагружения одного крюка

Определим геометрические характеристики сечения А-А для расчёта номинального значения напряжений в крюке. Сечение А-А представлено на рис. 35.

Рис. 35 – Расчётное сечение крюка

Рассчитаем необходимые для расчёта номинального значения напряжений геометрические характеристики приведённого на рис. 35 сечения:

м²;

м⁴;

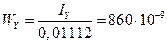м³.

Определим номинальное значение напряжения:

МПа.

Тогда теоретический коэффициент концентрации напряжений будет равен

.

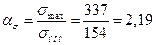Блок нагружения, представленный на рис. 31, содержит напряжения, вызванные эксплуатационной нагрузкой и нагрузкой, равной половине эксплуатационной. Поэтому определим напряжения 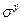и :

МПа;

МПа.

Следующим шагом оценки долговечности крюка удержания выводных рычагов является построение кривой усталости.

Определим значение предела выносливости при отнулевом цикле изменения напряжений. Приведение будем осуществлять по формуле Одинга. При этом константу , являющуюся характеристикой материала, примем равной 0,5:

.

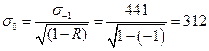Найдём значение коэффициента снижения предела выносливости для материала критической зоны. Для этого рассчитаем коэффициенты концентрации напряжений , влияния абсолютных размеров поперечного сечения , влияния шероховатости поверхности , влияния поверхностного упрочнения и анизотропии .

Для расчёта значения определим вспомогательные величины (значение принято равным 0,5 мм):

мм^-1;

.

Тогда получим:

.

Определим коэффициент :

.

Значения коэффициентов , и примем равными:

;

.

Проведём расчёт коэффициента :

.

С учётом полученного значения коэффициента снижения предела выносливости определим предел выносливости материала критической зоны при отнулевом цикле напряжения:

МПа.

Также найдём значение показателя наклона кривой усталости :

.

С учётом полученных характеристик кривой усталости рассматриваемой критической зоны крюка удержания выводных рычагов определим предельное количество циклов при напряжении :

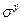цикла.

Значение 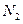не определяется ввиду выполнения условия .

Для расчёта запаса по долговечности определим значение коэффициента надёжности η. При этом примем следующие значения коэффициентов, входящих в каноническую формулу коэффициента надёжности η.

Так как при определении МНДС критической зоны использовался метод конечных элементов с исследованием сходимости результатов, то коэффициент принимаем минимальным из заданного диапазона и равным 1,2.

Исследуемый крюк выполнен из неоднородного материала (литьё). В то же время при расчёте МНДС характеристики материала задавались по минимальным значениям, приведённым в справочниках. Поэтому коэффициент принимаем равным 3,0.

В случае разрушения крюка работоспособность всей катапульты может быть нарушена. Следовательно, значение коэффициента принимаем равным 1,5.

Определим коэффициент надёжности η:

.

Последним этапом расчёта является определение запаса по долговечности:

.

Полученное значение позволяет сделать вывод, что крюк удержания выводных рычагов при заданных нагрузках и их повторяемости не разрушится. Усталостная прочность крюка обеспечена. Также величина , равная 28,3, позволяет сделать вывод, что исследуемый крюк может выдержать без разрушения до 28 заданных блоков нагружения.

Дата добавления: 2015-07-12