Задания к лабораторной работе

Варианты индивидуальных заданий

Задание: Составить алгоритм и программу для решения следующих задач.

№
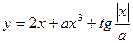	;		a=0.1 b=9.5
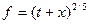
			t=10 x=1.1
			b=21 y=2.2
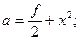
			f=3.2 x=1.4
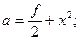
			f=42.5 x=10.2
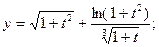
			x=-0.007
			a=2.3 x=0.2
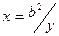
			b=3.7 y=1.02
			x=9.325
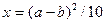
			a=7.25 b=3
			x=13.7
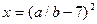
			a=5 b=3.25
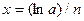
			a=7 n=4
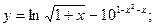
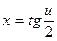
			u=3.47
			a=10.3
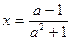
16			a=4.25
			a=1.25 b=3
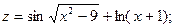
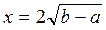
			a=7.2 b=5
			a=7.2 f=0.5
			a=4.25
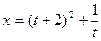
			t=3.2
			x=2
			a=4.2 b=2.7
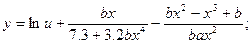
			a=2.25 b=10.27
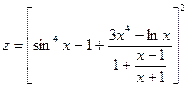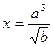
	;		a=2.25 b=10.27
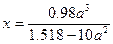
			a=1.5 b=1.2
			a=3 b=1.2
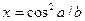
			a=24 b=1.9
			a=2.5 b=2a+3/1.5
			a=1.1 b=2

Задания к лабораторной работе

Составить алгоритм и программу для вычисления арифметических выражении

Варианты	Задания
	А	ìat^2lnt, если 1≤t ≤2 Y = í1, если t <1 îe^atcosbt, если t >2
Б	Даны два действительных числа х, у (х у). Если первое число больше второго, выдать признак N = 100, в противном случае N = 0.
	А	ìpx^2– 7/(x^2 +1), если x < 1,3 Y = íax^3 + 7 , если x = 1,3 îlg(x +7 ), если x > 1,3
Б	Даны три числа, возвести в квадрат те из них, значения которых неотрицательны, отрицательные числа оставить без изменения.
	А	ìax^2+ bx +c, если x <1, 2 Y = ía/x + , если x = 1,2 î(a + bx) , если x > 1,2
Б	Даны два числа а и в. Если а и в отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0,7; если оба значения неотрицательны, то оба значения увеличить в 10 раз.
	А	ì0, если 1≤t ≤2 Y = íat, если t <1 îe^at+ t^4, если t >2
Б	Даны действительные числа а, в, с. Удвоить эти числа, если а≥в≥c, заменить их абсолютными значениями, если это не так.
	А	ìsin x, если x< -0,8 Y = í1/sin x, если -0,8 ≤x ≤0,2 îsin x cos x, если x >0,2
Б	Даны три действительных числа l, m, n. Выбрать те из них, которые принадлежат интервалу (1;3).
	А	ì0, если x ≤0 Y = íx^2 - x, если 0 < x <1 îx^2 – sin px, в остальных случаях
Б	Даны действительные числа x, y, z. Вычислить U = max{x + y + z; xyz}
	А	ì1,5cos^2x, если x < 1 Y = í1,8ax, если x = 1 | (x –2)^2 +6, если 1< x < 2 î 3 tgx, в остальных случаях
Б	Даны действительные числа а, в, с. Вычислить Z = min^2 {(a + b + c)/ 2; abc} + 1,25
	А	ìx^3 , если x > a Y = íx sinax, если x = a îe^-^axcosax, в остальных случаях
Б	Даны три действительных числа. Выбрать те из них, которые принадлежат интервалу (1;5).
	А	ìbx -lgbx, если 0 < bx < 1 Y = í1, если bx = 1 îbx +lgbx, в остальных случаях
Б	Даны действительные числа x, y, z. Утроить эти числа, если x ≤ y≤z и заменить их абсолютными значениями, если это не так.
	А	ìcos x, если x < 2,3 Y = í1, если x = 2,3 î sin x lg x, в остальных случаях
Б	Даны действительные числа x, y, z. Вычислить U = max{(x+y) / z; xyz} +1,05 yz
	А	ì lg (x + 1), если x > 1,1 Y = í1, если x < 1,1 îsin^2 , в остальных случаях
Б	Даны три отличных от нуля числа, возвести в квадрат отрицательные, а положительные оставить без изменения.
	А	ìsin x lg x, если x > 2,5 Y = í1, если x = 2,5 îcos x, в остальных случаях
Б	Даны действительные числа а, в, с. Найти наименьшее из них: U = min{a, в, c}
	А	ìabc, если a < 2,7 Y = í(b+c)/a, если a = 2,7 î(2c+b)/a^2, в остальных случаях
Б	Если сумма трех попарно различных чисел x, y, z меньше 1, то меньшее из х и у заменить полусуммой у и z, иначе большее из х и z заменить на у^4.
	А	ìa lg x + , если x > 0,9 Y = í1, если x = 0,9 î2a cos x +3x^2, если х < 0,9
Б	Даны три числа l, m, n. Вычислить Z = min^3{l+m; m+n; l+n}-0,07lmn
	А	ì3a cos x, если x < 8,3 Y = í1/x^3, если x = 8,3 î sin x + lg x, в остальных случаях
Б	Даны три числа x, y, x. Вычислить U = min^2{x+y+z; xyz; x+2,5yz}

Дата добавления: 2015-07-12