Шаги реконструкции

Для реконструкции схемы циркуляции пневмы по меридианам следует использовать выявленную выше связь пневм и триграмм. Каждый меридиан при этом получит в соответствие одну из шести “младших” триграмм. Однако чтобы эти соответствия имели некоторую логическую строгость, необходимо сделать одно исправление, а именно каналы легких и селезенки отнести по классификации не к “великой инь ” (тай инь), а к “малой инь (шао инь) и, соответственно, каналы почек и сердца отнести не к “малой инь ”, а к “великой инь ” (табл. 2.3.11). Иначе говоря, при соотнесении триграмм с меридианами на основе их подразделений на три ян и три инь, следует совершить перестановку триграмм 010 и 011.

Таблица 2.3.11
Код	Пневмы	Меридианы
	Цзюе инь	Цзюе инь
	Шао инь	Тай инь
	Тай инь	Шао инь
	Шао ян	Шао ян
	Ян мин	Ян мин
	Тай ян	Тай ян

Это исправление позволяет показать, каким образом может быть построена схема циркуляции пневмы по меридианам. Для этого в качестве исходных используются два порядка триграмм, которые будут задавать “земной” и “небесный” (см. табл. 2.3.9) структурные компоненты пневматического цикла. Первый — порядок Фуси (В1), второй — “взаимопорождения” (А3). Последний порядок сдвинут на полпериода на базис-схеме (рис. 2.3.6) относительно положения в приводившихся выше его записях (см. рис. 2.2.4 и др.).

Рис. 2.3.6

Из порядка “взаимопорождения” методом “симметрично-дихотомического” деления (ср. рис. 2.2.14) получим “космогонический” порядок, точнее, два симметричных (обратный и прямой) “космогонических” порядка (рис. 2.3.7).

Рис. 2.3.7

Схему с порядком Фуси (рис. 2.3.6, B1) совместим с получившейся схемой, в которой янские и иньские меридианы, символизируемые триграммами из “космогонического” порядка, будут обозначаться соответственно белыми и черными кружками (рис. 2.3.8). Попутно отметим, что при этом обнаружится следующая закономерность: каждая триграмма из порядка Фуси охватывает две триграммы из “космогонического” порядка таким образом, что одна из них с нею совпадает (на схеме подчеркнута).

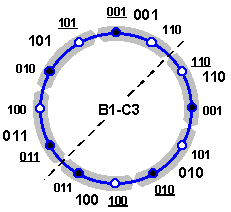
Рис. 2.3.8

Далее следует произвести симметричное преобразование порядка Фуси, подобное тому, что приводилось выше как способ получения “современного” порядка (см. рис. 2.2.15). Отличие заключается в том, что при данном преобразовании будут учитываться связи порядка Фуси с триграммами “космогонического” порядка. Для этого, во-первых, триграммы порядка Фуси надо отнести с шестеричных подразделений круга на двенадцатеричные, а во-вторых, чтобы при преобразовании сохранялись корреляции триграмм из порядков Фуси и “космогонического”, следует выделить диполи из “космогонического” порядка и привязать их к тем из двенадцатеричных подразделений, которые маркируются триграммами порядка Фуси (рис. 2.3.9).

Рис. 2.3.9

Затем производятся указанные выше преобразования, при которых с переносом триграмм на противоположные стороны схемы одновременно переносятся и связанные с ними диполи (рис. 2.3.10). При этом учитывается их расположение относительно хода времени (на схеме символизируется направлением по часовой стрелке): при переносе каждого диполя на противоположную сторону он разворачивается так, чтобы сохранялась его прежняя направленность во времени. В результате получается схема, символика которой и пространственно-временная ориентация совпадают со схемой циркуляции пневмы по меридианам.

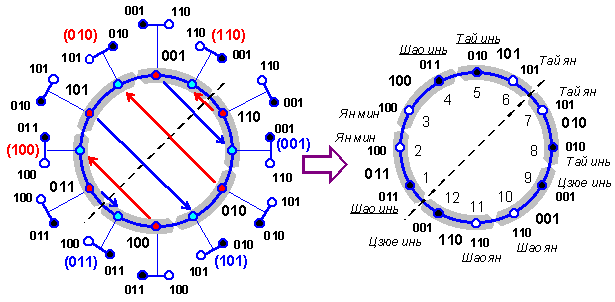
Рис. 2.3.10

Дата добавления: 2015-07-12