Схемы циклов

Для более удобного анализа древнекитайских мироописательных схем с арифмосемиотической символикой (триграммы, стихии, пневмы, циклические знаки и т.д.) в дальнейшем будет использоваться специальная схема описания — “базис-схема”, представляющая собой круг (символ циклически развивающихся процессов), который имеет несколько вариантов членения — простое двенадцатеричное членение, с объединением двенадцати частей круга по парам и шестеричное, при котором более дробные величины не существенны (рис. 2.2.3; северные циклические знаки здесь размещаются по китайскому образцу — внизу схемы).

Рис. 2.2.3

Если расположить порядки триграмм А-серии на базис-схеме, связав “младшие” триграммы с ее шестью элементами, то можно увидеть, что они преобразуются один в другой за счет сдвига триграмм по некоей внутренней фигуре, причем порядки триграмм размещаются как в по часовой стрелке, так и против нее (рис. 2.2.4).

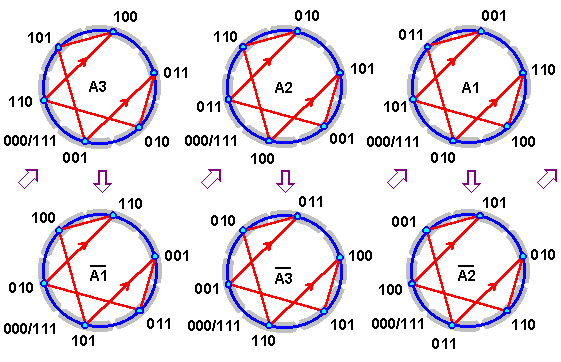
Рис. 2.2.4

Эта внутренняя фигура, которая далее будет называться “гексанемой” (гр. hex шесть + nema нить), интересна тем, что она не только часто встречается в тех или иных подвергшихся реконструкции древнекитайских арифмосемиотических схемах, отражая их инвариантные закономерности, но и является компонентом “эннеаграммы” (от гр. ennea — 9), предъявленной Г.И. Гюрджиевым (иное написание — Гурджиев; 1877—1949) на его лекциях в Европе и Америке и опубликованной, в частности, его последователем П.Д. Успенским в середине прошлого века (см.: Успенский 1999: 384, 393). По сведениям Г.И. Гюрджиева, схема эннеаграммы применялась в древнем мире для записи тайных знаний. К сожалению, более определенно о ее истоках он не высказывался. Однако на основании нижеприводимого комплекса исследований можно предположить, что эта схема в некоей своей первоначальной форме, отдельные стороны которой проступают в арифмосемиотике, была создана в Китае в западночжоускую эпоху. Можно также предположить, что со временем эннеаграмма проникла на Запад, где чудом сохранилась в одном из эзотерических учений, из которого и была заимствована Г.И. Гюрджиевым.

В самых общих чертах эннеаграмма представляет собой круг, на котором размещен ряд натуральных чисел от 1 до 9 (рис. 2.2.5). Эти числа играют в данной схеме роль специфической символики явлений, происходящих в определенных целостных образованиях, и подразделяются на два набора. Числа 1, 2, 4, 5, 7, 8 связаны друг с другом внутри круга линиями (которые и составляют гексанему) в следующем порядке: 1, 4, 2, 8, 5, 7... Остальные три числа — 3, 6, 9 — образуют треугольник. Набор из шести чисел в двух указанных порядках символизирует некие циркуляции “энергий” внутри взятых для символизирования целостностей, а троичный набор обозначает силы, приводящие в действие эти самые “энергии”.

Рис. 2.2.5

Гексанема является наиболее характерной деталью эннеаграммы. Она задается циклической дробью 1/7 = 0,[142857]. Следует отметить, что аналогичная циклическая последовательность образуется при делении на 7 любого целого числа (если, конечно, оно не кратно числу 7). При другом числителе начало периода просто сместится (например, 3/7 = 0,[428571]). Однако для получения данного периода необходимо, чтобы деление производилось в десятеричном счислении, и неизвестно, использовалось ли оно при создании эннеаграммы. С другой стороны, составляющую этот период последовательность чисел можно получить при делении на 7 круга, который при этом делится еще на десять частей, каждая из которых также делится на десять частей, делимых, в свою очередь, на десять частей и т.д. (рис. 2.2.6). Такое построение кажется более правдоподобным, учитывая общий уровень знаний в древности, но в этом случае “эннеаграмму” вернее было бы называть “декаграммой” (от гр. deka — 10).

Рис. 2.2.6

Следует отметить, что гексанему можно получить посредством деления круга на 7 не только в системе счисления с основанием 10. Основанием системы счисления, в которой образуется гексанема, является любое число n = (13 +7i)/2, если i = 1, 3, 5, 7..., или n = (10 + 7i)/2, если i = 2, 4, 6, 8... Например, если i = 2, то n = 12.

Деление круга на двенадцать частей используется в календаре и поэтому является особо интересным. При построении гексанемы на двенадцатеричном основании круг сначала делится на 12 частей, они также делятся на 12 частей и так до бесконечности. При последующем делении круга на 7 частей их величины можно будет выразить с любой точностью с помощью образовавшейся двенадцатеричной шкалы. Далее следует соединить линиями цифры, входящие в периодическую дробь 12/7 = 1,[8|6|10|3|5|1] и обозначающие либо границы соответствующих частей, получаемых при делении круга на 12, либо сами эти части (рис. 2.2.7). Образовавшуюся схему следует назвать “додекаграммой” (от гр. d` odeka — 12). Конкретным ее выражением в китайской арифмосемиотике может быть схема года, которая подразделялась китайцами как на 12 месяцев по 29 или 30 дней, так и на 28 периодов по числу лунных стоянок сю (см. табл. 1.5.3; рис. 1.5.1), которые можно разбить на 7 групп с 4-мя сю в каждой.

Рис. 2.2.7

Если не брать во внимание различия в символике, ракурс схемы и некоторые не отмеченные здесь несущественные подробности, то следует признать, что гексанема в гюрджиевской эннеаграмме, в реконструированных декаграмме и додекаграмме и гексанема, образуемая на круге “младших” триграмм, достаточно схожи по строению и функциям.

Триграммы можно представить в виде чисел от 0 до 7, и тогда сходство эннеаграммы и триграммных схем будет еще большим. Для этого надо поставить в соответствие янским знакам в позициях триграмм X, Y, Z числа 4, 2, 1, суммы которых в каждой триграмме определят соответствующее ей число (табл. 2.2.4).

Таблица 2.2.4
X Y Z
S

Несмотря на то, что шестеричная базис-схема с триграммами призвана иллюстрировать преобразования порядков шести “младших триграмм”, в ней латентно заложено представление о семеричности. “Старшие” триграммы, начинающие и заканчивающие эти порядки, можно рассматривать как смыкающиеся, и тогда все триграммы обозначат семь частей, на которые делится круг базис-схемы (рис. 2.2.8). Смычка Кунь / Цянь, не участвующая в преобразованиях, будет соответствовать тому лучу семилучевой звезды, с которого начинается деление. “Младшие” триграммы в соответствии со своими численными выражениями будут коррелировать с остальными лучами. Эти оставшиеся лучи попадают в зоны, на которые подразделяется круг при его шестеричном делении. Поэтому условно можно считать, что гексанема связывает именно эти шесть зон, а не пункты разбивки круга на семь частей.

Рис. 2.2.8

“Младшие” триграммы, выстраивающиеся по гексанеме на рассмотренных базис-схемах, образуют следующий замкнутый порядок: 100—110—010—011—001—101 (см. рис. 2.2.4, 2.2.8, ср. рис. 2.1.4). Его характерной особенностью является то, что он последовательно связывает триграммы, имеющие только одну позицию с различающимися знаками. В современной информатике связи двоичных кодов по принципу изменения знака только в одной позиции считаются наиболее энергетически выгодными, а сама операция по преобразованию кода подобным образом называется “шагом Хемминга”. Надо отметить, что для шести “младших” триграмм возможна только одна подобная связь, зафиксированная как раз в гексанеме. Образующийся на основе этой связи порядок триграмм далее будет называться “ротационным” или “ротатором” (R), исходя из того, что одной из его функций является участие в циклических сдвигах при преобразованиях других порядков триграмм.

Порядки триграмм В-серии также преобразуются друг в друга посредством сдвигов “ротатора” по гексанеме, но только этот сдвиг осуществляется в противоположном направлении (рис. 2.2.9).

Рис. 2.2.9

Перекодировка триграмм В-серии в числа должна иметь обратную корреляцию чисел 1, 2, 4 с позициями триграмм (табл. 2.2.5).

Таблица 2.2.5
X Y Z
S

В-серия, в которой находится порядок Фуси (В1), не включает в себя известные порядки стихий, представленные в корреляции с “младшими” триграммами (см. табл. 2.2.1). Эта серия проявляет себя в закономерностях взаимодействий шести пневм- ци,коррелирующих с триграммами (см. следующую главу). Напротив, в А-серии имеется два важнейших порядка стихий — “взаимопорождение” (А3) и “взаимопреодоление” (А1). Для удобства далее соответствующие порядки триграмм будут именоваться аналогично.

То, что при корреляции стихий с шестью “младшими” триграммами образуются также шестеричные порядки стихий, вовсе не мешает соотнести последние с пятеричными. Стихии коррелируют с триграммами так, что две “младшие” триграммы (001 и 110) оказываются связанными с деревом. Однако в рассматриваемых порядках триграмм они стоят рядом и при этом взаимодействуют одновременно по принципам “взаимопорождения” и “взаимопреодоления”, которые нейтрализуют друг друга, приводя к уменьшению различий между взаимодействующими триграммами. Поэтому эти триграммы и могут быть связаны с одной стихией, а шестеричный порядок стихий может быть преобразован в пятеричный. При таком преобразовании получится классическая пентаграмма, в которой по кругу стихии располагаются в порядке “взаимопорождения”, а по звезде — в порядке “взаимопреодоления” (рис. 2.2.10; ср. рис. 1.3.4).

Рис. 2.2.10

Таким образом, в учении о стихиях зафиксированы частные закономерности взаимодействия триграмм. По всей видимости, пятеричный набор стихий в порядке “взаимопорождения” может отражать тот же самый процесс развития неких реалий, что и триграммный порядок А3, но только с учетом запаздывания. Если началом процесса полагать стихию “дерево”, а полные периоды развития пятеричного и шестеричного наборов стихий принять одинаковыми по времени, то получится, что каждая другая стихия доходит до кульминации своего развития в пятеричном порядке несколько позже, чем в шестеричном. С другой стороны, если считать фазы развития отдельных стихий в шестеричном и пятеричном наборах одинаковыми, пятеричный цикл будет заканчиваться раньше, чем шестеричный, и новый пятеричный цикл также будет начинаться раньше предыдущего со сдвигом на одну стихию, как это происходит в китайском календаре (ср. табл. 1.5.4—6).

Такое свойство шестеричного порядка обусловлено, видимо, тем, что он, выделенный из целостной системы триграмм, мыслится сам по себе, без соотнесения с другими порядками, которые через множество взаимосвязей могут препятствовать или способствовать как его развитию в целом, так и смыканию триграмм 001 и 110, коррелирующих с одной и той же стихией. Кроме того, рассматривая шестеричный порядок в контексте восьмеричного набора триграмм, следует учитывать, что триграмма Цянь обозначает некий источник энергии, который осуществляет подпитку процесса, символизируемого “младшими” триграммами. Пятеричный же набор стихий, согласно традиционной теории, не имеет дополнительного источника энергии, поэтому символизируемый им процесс затухает быстрее.

Аналогичные рассуждения справедливы и для порядков В1 и В3, которые имеют структурные отношения, подобные отношениям порядков А3 и А1.

Дата добавления: 2015-07-12