|
Читайте также: |
Вопросы:
Вопрос 1. Понятие корреляционно-регрессионного анализа
В статистических распределениях всегда присутствует более или менее значительная вариация в величине признака у отдельных единиц совокупности. Возникает вопрос о причинах (факторах), формирующих уровень признака, и о вкладе каждой причины (фактора) в уровень признака.
Содержанием теории корреляции является изучение зависимости признака от окружающих условий.
Основоположниками теории корреляции являются английские ученые Фрэнсис Гальтон (1822-1911); математик и биолог Карл Пирсон (1857-1936).
Из практики известно, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность.
Например, вариация производительности труда зависит от степени совершенства применяемого оборудования, технологии, организации производства и др.
При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков-результатов.
Статистические показатели могут состоять между собой в факторных связях.
Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. Одни показатели – факторные, другие – результативные.
В свою очередь факторные связи могут быть:
· Функциональные;
· Корреляционные.
Функциональная связь: изменение результативного признака у всецело обусловлено
действием факторного признака х:
у = f(x) (1)
Функциональная связь проявляется с одинаковой силой у каждой единицы изучаемой совокупности. Знание функциональной зависимости позволяет абсолютно точно прогнозировать события (например, наступление солнечных затмений прогнозируется с точностью до секунды).
Корреляционная связь (correlation – соотношение) – изменение результативного признака у обусловлено не только изменением факторного признака х, а влиянием и прочих факторов ε:
у = ψ(x)+ ε (2)
Корреляционные связи - это связи соотносительные. Они не являются полными (жесткими) зависимостями. При одном значении факторного признака х в случае корреляционной связи возможны разные значения результативного признака у.
Корреляционные связи проявляются не в единичных случаях, а в массе. Они изучаются по статистическим данным.
Понятие корреляционно-регрессионного анализа.
Изучение связи показателей коммерческой деятельности необходимо не только для установления факта наличия связи. Определение механизма рыночных связей, взаимодействия спроса и предложения имеет первостепенное значение для прогнозирования конъюнктуры рынка и решения многих вопросов успешного ведения бизнеса.
Если две переменные связаны так, что изменению одной переменной х соответствует систематическое изменение другой переменной у, то для вывода уравнения, с помощью которого оценивается величина одной переменной, если величина другой известна, можно применять регрессионный анализ. В отличие от него корреляционный анализ применяется для нахождения и выражения тесноты связи между этими двумя переменными.
Более строго: если при каждом значении х=хi наблюдается ni значений уi1,..., yini величины у, то зависимость средних арифметических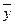 
=(yi1+... +yini)/ni от xi и является регрессией в статистическом понимании этого термина.
Перед статистикой в корреляционно-регрессионном анализе ставятся задачи:
Вопрос 2. Анализ связи парной корреляции
Наиболее разработанным в теории статистики является анализ парной корреляции, рассматривающий влияние вариации факторного признака х на результативный у.
1. В основу выявления формы связи положено применение в анализе исходной информации математических функций – уравнения прямолинейной и криволинейной связи.
Основой выявления формы связи является синтез адекватной экономико-математической модели (или уравнения регрессии). Выбор математической функции, адекватно отображающей экономические данные, производится перебором наиболее часто применяемых в анализе парной корреляции уравнений регрессии:
уx = а0 + а1 х, (прямолинейная зависимость) (3)
уx = а0 + а1 lgx, (полулогарифмическая) (4)
уx = а0 + а 1x, (показательная) (5)
уx = а0 + а0хa1, (степенная) (6)
уx = а0 + а1x + а2 х2, (параболическая) (7)
и другие.
Смысловое содержание этих моделей: они характеризуют среднюю величину результативного признака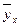 
в зависимости от вариации признака-фактора х.
2. Решение уравнений связи предполагает вычисление по исходным данным их параметров. Параметры уравнения регрессии а0 и а1 вычисляются методом наименьших квадратов.
Основа этого метода – требование минимальности сумм квадратов отклонений эмпирических данных уi от выровненных - теоретических ухi.
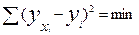(8)
Например, в случае линейной регрессии, параметры исчисляются по формулам:
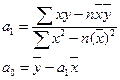(9)
а0 - сдвиг;
а1 - наклон (коэффициент регрессии). При наличии прямой корреляционной зависимости коэффициент регрессии имеет положительное значение, а в случае обратной зависимости коэффициент регрессии – отрицательный.
Коэффициент регрессии показывает, на сколько в среднем изменяется величина результативного признака у при изменении факторного признака х на единицу. Геометрически коэффициент регрессии представляет собой наклон прямой линии, изображающей уравнение корреляционной зависимости, относительно оси х.
Применение понятий. Интерпретация параметров уравнения регрессии.
Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством S&P (Standard and Poor), на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: уx = -5,0 + 7 х
Какой смысл имеют параметры сдвига и наклона?
Сдвиг регрессии равен -5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастет на 7%.
3. Полученные параметры уравнения регрессии необходимо испытать на их типичность. Так проверяется, насколько вычисленные параметры характерны для отображаемого комплекса условий. Не являются ли они результатами действия случайных причин.
Если в совокупности n < 30 (что характерно для малого и среднего бизнеса), для проверки типичности используется t-критерий Стьюдента.
При этом вычисляются значения t-критерия:
для параметра а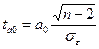0 
(10)
для параметра а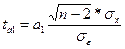1 
(11)
где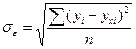 
- среднее квадратическое отклонение результативного признака уi от выровненных значений ухi; (12)
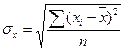- среднее квадратическое отклонение факторного признака хi от общей средней 
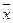. (13)
ta0 и ta1 сравниваются с критическим tk, полученным по таблице Стьюдента, с учетом принятого уровня значимости α и числа степеней свободы k=n-2.
Параметры уравнения регрессии признаются типичными, если
ta0 > tk < ta1 (14)
Мы должны обосновать применение метода функционального анализа при изучении корреляционной зависимости. Для этого докажем, что применение метода функционального анализа при изучении корреляционной зависимости не дает существенных погрешностей.
Это осуществляется посредством показателей тесноты связи между признаками х и у.
Для статистической оценки тесноты связи между признаками х и у применяются следующие показатели вариации:
1) Общая дисперсия результативного признака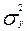 
, отображающая совокупное влияние всех факторов
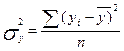, (15)
где уi - эмпирические значения
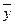- общая средняя теоретических (выровненных) значений.
Отклонения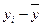 
обусловлены тем, что сочетание факторов, влияющих на вариацию признака у, для каждой единицы анализируемой совокупности различно.
2) Факторная дисперсия результативного признака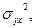 
отображающая вариацию результата у только от воздействия изучаемого фактора х
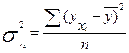, (16)
где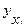 
- теоретические (выровненные) значения.
Факторная дисперсия характеризует отклонения выровненных значений от их общей средней величины.
3) Остаточная дисперсия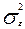 
отображает вариацию результативного признака у от всех прочих, кроме х, факторов
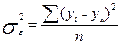. (17)
Остаточная дисперсия характеризует отклонения эмпирических (фактических) значений результативного признака у от их выровненных значений .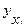
5. Индекс детерминации (причинности) R2 выражает долю факторной дисперсии в общей дисперсии
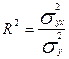. (18)
Индекс корреляции R (эмпирическое корреляционное отношение) находится из (18)
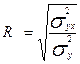, (19)
Используя правило сложения дисперсии: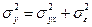 
, (20)
индекс корреляции можно вычислить по следующей формуле:
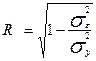. (21)
При прямолинейной форме связи определяется линейный коэффициент корреляции r:
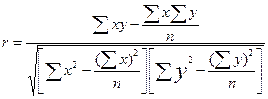. (22)
6. Показатели тесноты связи для небольших статистических совокупностей могут искажаться действием случайных причин, поэтому возникает необходимость проверки их существенности.
Для оценки значимости r (линейного коэффициента корреляции), применяется t – критерий Стьюдента. Определяется фактическое значение критерия:
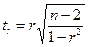(23)
Далее рассчитанное значение критерия tr сравнивается с критическим tk, взятым из таблицы Стьюдента с учетом α(уровня значимости) и k(числа степеней свободы).
Если tr > tk, то величина линейного коэффициента корреляции r - существенна.
Для оценки значимости R (эмпирического корреляционного отношения), применяется F – критерий Фишера. Определяется фактическое значение критерия:
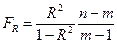(24)
Здесь m – число параметров уравнения регрессии.
Далее рассчитанное значение критерия FR сравнивается с критическим Fk из таблицы F - критерия с учетом α(уровня значимости) и k1 = m-1; k2 = n-m (числа степеней свободы)
Если FR > Fk, то величина эмпирического корреляционного отношения R - существенна.
7. Для получения выводов о практической значимости синтезированных в анализе моделей показаниям тесноты связи даётся качественная оценка по шкале Чеддока:
| Показания тесноты связи | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | cлабая | умеренная | заметная | высокая | весьма высокая |
При значении показателя равном 1 имеет место функциональная связь.
При значении показателя равном 0 связь отсутствует.
Если, например, значение показателя тесноты связи R2 > 0,7(индекс детерминации), это означает, что более половины общей вариации результативного признака у объясняется влиянием изучаемого фактора х.
8. Для оценки адекватности уравнения регрессии можно использовать показатель средней ошибки аппроксимации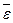 
:
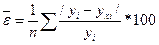(25)
Здесь /уi - yxi / линейные отклонения абсолютных величин эмпирических и выровненных точек регрессии.
Если 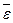минимальна, то соответствующая математическая модель является наиболее адекватной для практических целей (прогнозирования в регрессионном анализе: интерполяция и экстраполяция).
Применение понятий:
Сеть магазинов одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представление менеджера об идеальном местоположении магазина. Представьте себе, что вы – руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Наша цель – предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом годовых продаж создадим выборки из 14 магазинов:
Таблица. Площади и годовые объемы продаж 14 магазинов сети Sunflowers
| Магазин | Площадь | Годовые продажи |
| 1,7 | 3,7 | |
| 1,6 | 3,9 | |
| 2,8 | 6,7 | |
| 5,6 | 9,5 | |
| 1,3 | 3,4 | |
| 2,2 | 5,6 | |
| 1,3 | 3,7 | |
| 1,1 | 2,7 | |
| 3,2 | 5,5 | |
| 1,5 | 2,9 | |
| 5,2 | 10,7 | |
| 4,6 | 7,6 | |
| 5,8 | 11,8 | |
| 4,1 |
Диаграмма разброса представлена на рис.
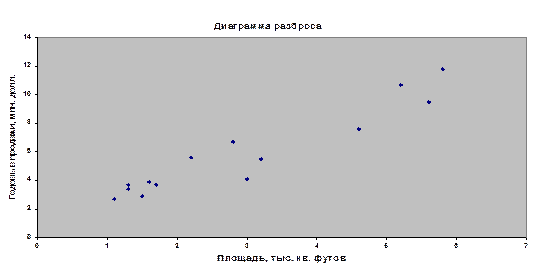
Между площадью магазина Х и годовым объемом продаж У можно предположить наличие положительной зависимости.
Произведем синтезирование адекватной экономико-математической модели в виде линейной зависимости.
уx = а0 + а1 х
Для определения параметров линейной зависимости построим вспомогательную таблицу:
| Магазин | Площадь Х | Годовые продажи У | Х2 | ХУ | Теоретические Ух |
| 1,7 | 3,7 | 2,89 | 6,29 | 3,803 | |
| 1,6 | 3,9 | 2,56 | 6,24 | 3,636 | |
| 2,8 | 6,7 | 7,84 | 18,76 | 5,640 | |
| 5,6 | 9,5 | 31,36 | 53,2 | 10,316 | |
| 1,3 | 3,4 | 1,69 | 4,42 | 3,135 | |
| 2,2 | 5,6 | 4,84 | 12,32 | 4,638 | |
| 1,3 | 3,7 | 1,69 | 4,81 | 3,135 | |
| 1,1 | 2,7 | 1,21 | 2,97 | 2,801 | |
| 3,2 | 5,5 | 10,24 | 17,6 | 6,308 | |
| 1,5 | 2,9 | 2,25 | 4,35 | 3,469 | |
| 5,2 | 10,7 | 27,04 | 55,64 | 9,648 | |
| 4,6 | 7,6 | 21,16 | 34,96 | 8,646 | |
| 5,8 | 11,8 | 33,64 | 68,44 | 10,650 | |
| 4,1 | 12,3 | 5,974 | |||
| Итого | 40,9 | 81,8 | 157,41 | 302,3 | |
| В среднем | 2,921 | 5,843 |
С использование формул и результатов расчета из табл. найдем параметры:
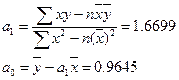
Полученная экономико-математическая модель примет вид:
уx = 0,9645 + 1,6699* х
Проверим результаты расчетов с помощью Пакета Анализа Excel (Сервис-Анализ данных-Регрессия).
Результаты решения задачи о зависимости между площадями и годовыми объемами продаж помощью Пакета Анализа:
| Анализ данных о магазинах | ||
| Регрессионная статистика | ||
| Множественный R | 0,95088 | эмпирическое корреляционное отношение или индекс корреляции |
| R-квадрат | 0,90418 | индекс детерминации |
| Нормированный R-квадрат | 0,89619 | |
| Стандартная ошибка | 0,96638 | |
| Наблюдения | ||
| Дисперсионный анализ | ||
| df | SS | |
| Регрессия | факторное отклонение 105,747609504616 | |
| Остаток | остаточное отклонение 11,2066762096698 | |
| Итого | общее отклонение 116,954285714286 | |
| Коэффициенты | Стандартная ошибка | |
| Y-пересечение | а0 сдвиг=0,964473659427793 | 0,52619 |
| Площадь | а1 коэффициент регрессии (наклон)=1,66986231706628 | 0,15693 |
Представим уравнение линейной регрессии зависимости годовых объемов продаж У от площади магазина Х в виде графика:
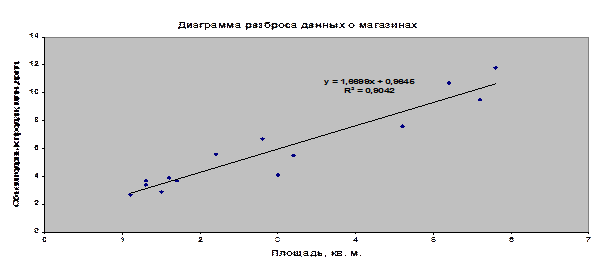
Проверим параметры полученного уравнение регрессии на типичность:
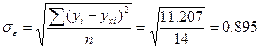- среднее квадратическое отклонение результативного признака уi от выровненных значений ухi;
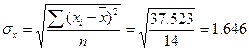- среднее квадратическое отклонение факторного признака хi от общей средней .
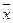Вычислим значения t-критерия:
для параметра а0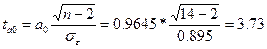 
для параметра а1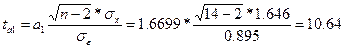 
Далее ta0 и ta1 сравниваются с критическим tk = 2,18, полученным по таблице Стьюдента, с учетом принятого уровня значимости α=0,05 или 5% и числа степеней свободы k=14-2=12.
Параметры уравнения регрессии признаются типичными, т.к.
ta0 > tk < ta1
Оценим практическую значимость синтезированной модели (с помощью линейного коэффициента корреляции):
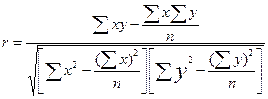
Для его определения имеющуюся таблицу со вспомогательными расчетами дополним недостающими показателями. Тогда r = 0.95. Это значение больше нуля. Поэтому между площадью магазинов и суммой годовых продаж существует прямо пропорциональная зависимость.
По шкале Чеддока: установленная по уравнению регрессии связь между площадью магазина и суммами продаж весьма высокая.
Оценим значимость r (линейного коэффициента корреляции).
Применим для этого t – критерий Стьюдента.
Определим фактическое значение критерия:
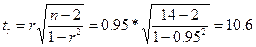
Далее рассчитанное значение критерия tr сравнивается с критическим tk =2,18 из таблицы Стьюдента с учетом α=0,05 (уровня значимости) и k=14-2 (числа степеней свободы)
tr > tk, поэтому величина вычисленного линейного коэффициента корреляции r признается существенной.
Исчислим для проверки линейный коэффициент корреляции с помощью Пакета Анализа Excel (Сервис-Анализ данных-Корреляция):
| Площадь | Годовые продажи | |
| Площадь | ||
| Годовые продажи | 0,950883275 |
Выводы: 0,952 = 0,9025. Поэтому более 90% общей вариации годовых продаж объясняется изменением площади магазинов (факторного признака). Между площадью и годовыми продажами существует весьма тесная прямая зависимость. С повышением площади магазинов их годовые продажи стремятся к увеличению. Синтезированная с помощью уравнения регрессии математическая модель м.б. использована для практических целей.
Дата добавления: 2015-07-12; просмотров: 96 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вопрос 2. Агрегатные индексы. | | | Прогнозирование в регрессионном анализе: интерполяция и экстраполяция |