
Читайте также:
|
С понятием множества многие из вас хорошо знакомы из школьного курса математики. Вам известно, что понятие множества является первичным в математике и через другие понятия не определяется; что множества принято обозначать заглавными буквами латинского алфавита, а элементы множества малыми буквами; над множествами можно осуществлять операции объединения, пересечения и вычитания. Те кому, это необходимо, могут повторить (изучить) основные сведения по теории множеств, используя, [1], стр. 5 -7 или [2], стр. 9-13 (смотрите список литературы, рекомендуемой для подготовки к экзамену).
Множества, элементами которых являются числа, называются числовыми множествами. Как правило, при изучении математики в школе, ограничиваются использованием следующих числовых множеств:
 - множество натуральных чисел;
- множество натуральных чисел;
 - множество целых чисел;
- множество целых чисел;
 - множество рациональных чисел;
- множество рациональных чисел;
R – множество действительных или вещественных чисел,
Множество действительных чисел R, чаще всего, вводится либо как множество бесконечных десятичных дробей [2], стр.13-27, либо как некоторая совокупность, где определены взаимосвязанные операции сложения, умножения, сравнения чисел по величине и которые обладают определенного рода непрерывностью [1], стр. 16-33. С формальной точки зрения оба подхода одинаковы, так как если число является действительным по первому определению, то оно действительно и по второму определению, и наоборот. Доказательство этого факто изложено в [2], стр. 27-28. С философской точки зрения более приемлемым является второй подход, так как числа – абстракции, выражающие количественные отношения реального мира, а десятичные дроби – символы, их представляющие. С другими подходами к определению действительного числа можно ознакомиться в Математической энциклопедии, т.2, стр. 74-78.
Рассмотренные выше множества связаны соотношениями:
 . (1)
. (1)
Однако, для практических приложений этих множеств недостаточно. Рассмотрим простейшее квадратное уравнение: 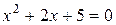 . Как известно, дискриминант этого уравнения
. Как известно, дискриминант этого уравнения 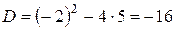 . И, следовательно, на множестве действительных чисел данное уравнение решений не имеет.
. И, следовательно, на множестве действительных чисел данное уравнение решений не имеет.
Если ввести число  , называемое мнимой единицей и обладающее свойством:
, называемое мнимой единицей и обладающее свойством:
 , (2)
, (2)
то дискриминант рассматриваемого выше уравнения можно представить в виде: 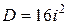 . Это позволит представить решение рассматриваемого уравнения в виде:
. Это позволит представить решение рассматриваемого уравнения в виде: 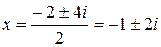 .
.
Решения уравнения представляют собой числа новой структуры, которые называются комплексными числами. Таким образом, мы имеем еще одно множество чисел. Введем определение этого множества с учетом сложившейся системы обозначений.
Определение 1. Множество чисел  называется множеством комплексных чисел.
называется множеством комплексных чисел.
Обозначение: 
Для каждой части комплексного числа  используется специальное название и обозначение:
используется специальное название и обозначение:
 - действительная часть комплексного числа z,
- действительная часть комплексного числа z,
 - мнимая часть комплексного числа z,
- мнимая часть комплексного числа z,
(от латинских слов: realis – действительный, imaginarius – мнимый).
Допускается запись комплексных чисел и в виде:  . Очевидно, что
. Очевидно, что
 . (3)
. (3)
Заметим, что  - действительное число,
- действительное число,  - чисто мнимое число,
- чисто мнимое число,  .
.
При введении любого множества сначала определяют, какие элементы этого множества считаются равными.
Определение 2. Комплексные числа 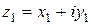 и
и  называются равными, если
называются равными, если  т.е. если у них совпадают действительные и мнимые части.
т.е. если у них совпадают действительные и мнимые части.
Обозначение:  .
.
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Определение 3. Суммой комплексных чисел 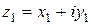 и
и  называется число z, определяемое по правилу:
называется число z, определяемое по правилу: 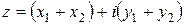 .
.
Обозначение: 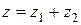 или
или
 . (4)
. (4)
Пример 1. Если 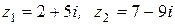 , то
, то
 .
.
Определение 4. Разностью комплексных чисел 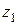 и
и  называется число z, такое что
называется число z, такое что  .
.
Обозначение: 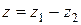 .
.
Теорема 1. Если  , то
, то
 . (5)
. (5)
Доказательство. Пусть  является разностью чисел
является разностью чисел  и
и  .
.
Тогда из определения разности (смотрите определение 4) следует, что  . Из определения суммы (смотрите определение 3) следует, что
. Из определения суммы (смотрите определение 3) следует, что 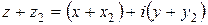 , учитывая, что это число должно быть равно числу
, учитывая, что это число должно быть равно числу 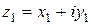 , получаем систему
, получаем систему  Решая систему, получаем нужный результат:
Решая систему, получаем нужный результат:  Что и требовалось доказать.
Что и требовалось доказать.
Пример 2. Если 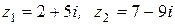 , то
, то
 .
.
Определение 5. Произведением комплексных чисел 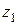 и
и  называется число z, определяемое по правилу:
называется число z, определяемое по правилу:  .
.
Обозначение:  или
или
 . (6)
. (6)
Определение 6. Частным от деления комплексного числа 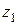 на комплексное число
на комплексное число  называется число z, такое что
называется число z, такое что 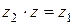 .
.
Обозначение: 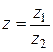 .
.
Теорема 2. Если  , где
, где 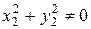 ; то
; то
 . (7)
. (7)
Доказательство. Пусть  - частное отделениячисла
- частное отделениячисла 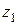 на число
на число  . Тогда, по определению частного (смотрите определение 6), следует, что
. Тогда, по определению частного (смотрите определение 6), следует, что 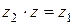 . Из правила умножения комплексных чисел (смотрите определение 5) следует, что
. Из правила умножения комплексных чисел (смотрите определение 5) следует, что  . Так как это число должно быть равно
. Так как это число должно быть равно 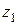 , получаем систему:
, получаем систему:
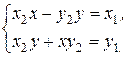 (8)
(8)
Умножая первое уравнение системы (8) на  , а второе уравнение на
, а второе уравнение на 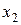 (это позволит уравнять коэффициенты при неизвестной х), получим систему (9):
(это позволит уравнять коэффициенты при неизвестной х), получим систему (9):
 (9)
(9)
Вычитая из второго уравнения системы (9) первое уравнение, имеем:
 ,
, 
 ,
, 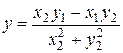 .
.
Для определения неизвестной х, умножаем первое уравнение системы (8) на 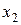 , а второе уравнение на
, а второе уравнение на  , получаем систему (10):
, получаем систему (10):
 (10)
(10)
Складывая уравнения системы (10), имеем:
 ,
,  ,
,  .
.
Теорема доказана.
Операции сложения и умножения комплексных чисел обладают следующими свойствами.
Теорема 3. Для любых  :
:
1)  - коммутативность;
- коммутативность;
2)  - ассоциативность;
- ассоциативность;
3)  - коммутативность;
- коммутативность;
4) 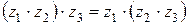 - ассоциативность;
- ассоциативность;
5)  - дистрибутивность.
- дистрибутивность.
Доказательство (проведите самостоятельно).
Данные свойства аналогичны свойствам операций сложения и умножения на множестве действительных чисел, поэтому на множестве комплексных чисел остаются справедливыми все правила проведения тождественных преобразований и формулы сокращенного умножения, справедливые на множестве действительных чисел.
Это дает возможность при проведении расчетов с комплексными числами не использовать формулы (6) и (7) для определения произведения и частного комплексных чисел, а рассматривать их как биномы (двучлены) и применять, привычные правила раскрытия скобок и приведения подобных членов, учитывая, что 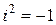 ,
,  ,
, 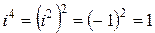 ….
….
В частности, практические правила определения произведения и частного выглядят так. Если 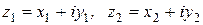 , то
, то


Пример 3. Если 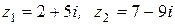 , то
, то


Определение 7. Комплексное число 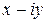 называют комплексным числом, сопряженным числу
называют комплексным числом, сопряженным числу 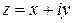 .
.
Обозначение: 

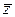 или
или
 . (11)
. (11)
Следовательно, чтобы определить частное от деления 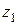 на
на  (
( ), достаточно числитель и знаменатель дроби
), достаточно числитель и знаменатель дроби  умножить на число, сопряженное
умножить на число, сопряженное  .
.
Определение 8. Модулем комплексного числа 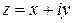 называется число, определяемое по правилу
называется число, определяемое по правилу  .
.
Обозначение:  или
или
 . (12)
. (12)
Теорема 3. Для любого комплексного числа 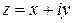
 . (13)
. (13)
Доказательство.  .
.
Рассмотренная форма записи комплексного числа называется алгебраической формой записи комплексного числа. А приведенные выше формулы (4) – (7) для выполнения операций сложения, вычитания, умножения и деления комплексных чисел называются правилами выполнения действий над комплексными числами, представленными в алгебраической форме.
Заметим, что каждому комплексному числу 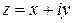 можно поставить в соответствие пару чисел
можно поставить в соответствие пару чисел 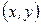 и наоборот. Это дает возможность для следующих двух вариантов геометрической интерпретации комплексных чисел.
и наоборот. Это дает возможность для следующих двух вариантов геометрической интерпретации комплексных чисел.
1 способ (как точки координатной плоскости). Зафиксируем на плоскости прямоугольную систему координат, обозначив начало координат О, а оси соответственно ОХ и ОУ (рисунок 1). Каждому комплексному числу 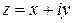 поставим в соответствие точку Р с координатами
поставим в соответствие точку Р с координатами 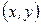 (рисунок 2). Получающаяся в этом случае плоскость называется комплексной плоскостью, ось ОХ –действительной осью, ось ОУ – мнимой осью.
(рисунок 2). Получающаяся в этом случае плоскость называется комплексной плоскостью, ось ОХ –действительной осью, ось ОУ – мнимой осью.


Рисунок 1 – Прямоугольная система Рисунок 2 – Изображение числа z
координат в виде точки
Пример 4. Изобразить на комплексной плоскости числа  ,
,  ,
,  ,
,  .
.
Согласно правилу числам  необходимо поставить в соответствие точки
необходимо поставить в соответствие точки  . Результат представлен на рисунке 3.
. Результат представлен на рисунке 3.


Рисунок 3 – Изображение чисел Рисунок 4 – Изображение числа z
в виде радиус-вектора точки




 2 способ (в виде радиус-вектора точки). В этом случае, зафиксировав на плоскости прямоугольную систему координат (рисунок 1), каждому комплексному числу
2 способ (в виде радиус-вектора точки). В этом случае, зафиксировав на плоскости прямоугольную систему координат (рисунок 1), каждому комплексному числу 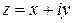 ставят в соответствие вектор
ставят в соответствие вектор  , т.е. радиус-вектор точки
, т.е. радиус-вектор точки  (рисунок 4).
(рисунок 4).
Заметим, что модуль вектора  по величине равен
по величине равен  , т.е. модулю комплексного числа
, т.е. модулю комплексного числа 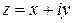 . Вводя обозначение:
. Вводя обозначение:
 , (14)
, (14)
получаем:
 . (15)
. (15)
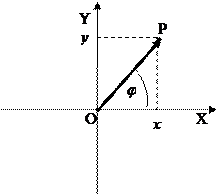



Рисунок 5 – Аргумент z Рисунок 6 - Треугольники
Определение 9. Угол  (рисунок 5), образованный радиус-вектором
(рисунок 5), образованный радиус-вектором  (
(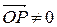 ) с положительным направлением оси ОХ(точнее угол поворота положительного направления оси ОХ до совмещения с радиус-вектором
) с положительным направлением оси ОХ(точнее угол поворота положительного направления оси ОХ до совмещения с радиус-вектором  ), называется аргументом числа z). Положительным считается направление обхода против хода часовой стрелки/
), называется аргументом числа z). Положительным считается направление обхода против хода часовой стрелки/
Обозначение:  .
.
Для  аргумент не определяется. Так как для
аргумент не определяется. Так как для  аргумент можно определить лишь с точностью до
аргумент можно определить лишь с точностью до  , то выделяют главное значение аргумента
, то выделяют главное значение аргумента  , как правило, это значения
, как правило, это значения  , хотя встречаются ситуации, когда выбирают
, хотя встречаются ситуации, когда выбирают  .
.
Обозначение: 
Очевидно, что
 (16)
(16)
Пусть у комплексного числа 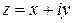
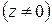
 . Для получения связи между
. Для получения связи между 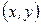 и
и  рассмотрим сначала случай, когда
рассмотрим сначала случай, когда  , т.е. когда радиус-вектор располагается в первой четверти.
, т.е. когда радиус-вектор располагается в первой четверти.
Рассматривая треугольники OLP и OPM (рисунок 6), где L – основание перпендикуляра, опущенного из точки Р на ось ОY, а M – основание перпендикуляра, опущенного из точки Р на ось ОХ, и учитывая, что 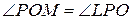 , как накрест лежащие при параллельных прямых, получаем:
, как накрест лежащие при параллельных прямых, получаем:
 ;
;  .
.
Аналогичные результаты будут иметь место и для остальных значений j (проверить самостоятельно).
Следовательно, для любого комплексного числа 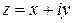
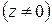 ,
,  имеют место соотношения (17):
имеют место соотношения (17):
 (17)
(17)
где r определяется по формуле (15),
 (18)
(18)
Используя формулы (17), получаем, что
 .
.
Определение 9. Представление комплексного числа 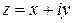
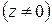 в виде
в виде 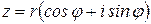 , где
, где  , называется тригонометрической формой записи комплексного числа z.
, называется тригонометрической формой записи комплексного числа z.
Пример 5. Представить число комплексное число  в тригонометрической форме.
в тригонометрической форме.
На практике, как правило, применяются два алгоритма: аналитический или геометрический (графический).
1 способ (аналитический). В этом случае сначала определяют модуль комплексного числа: 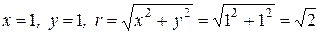 ; затем, используя формулы (18) определяют
; затем, используя формулы (18) определяют 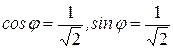 . С помощью которых однозначно определяется главное значение аргумента
. С помощью которых однозначно определяется главное значение аргумента  из промежутка
из промежутка  :
: 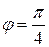 . Это означает, что
. Это означает, что 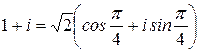 .
.
Заметим, что найдя модуль комплексного числа  , его можно было преобразовать так:
, его можно было преобразовать так:  , откуда сразу следует, что
, откуда сразу следует, что 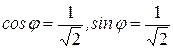 , и нет необходимости использовать формулы (18).
, и нет необходимости использовать формулы (18).
2 способ (геометрический). Отмечаем на комплексной плоскости точку P (1;1) и радиус-вектор  (рисунок 7).
(рисунок 7).



Рисунок 7 – Геометрическая Рисунок 8 – Треугольники
интерпретация числа 
Обозначив точкой L основание перпендикуляра, опущенного из точки Р на ось OY, точкой М – основание перпендикуляра, опущенного из точки Р на ось ОХ, получим квадрат OLPM со стороной 1. Длина диагонали ОР квадрата, равна модулю вектора 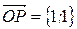 , и, следовательно, модуль комплексного числа равен длине диагонали квадрата, т.е.
, и, следовательно, модуль комплексного числа равен длине диагонали квадрата, т.е.  . Главное значение аргумента числа
. Главное значение аргумента числа  совпадает с величиной угла
совпадает с величиной угла  , а угол между диагональю квадрата и стороной квадрата равен
, а угол между диагональю квадрата и стороной квадрата равен  , следовательно,
, следовательно,  . Таким образом,
. Таким образом, 
Тригонометрическая форма записи комплексных чисел упрощает вид формул для выполнения операций умножения, деления и возведения в степень.
Теорема 4. Если  , где
, где  , то
, то
1)  ; (19)
; (19)
2)  ; (20)
; (20)
3)  (21)
(21)
Доказательство. Формулы (19) и (20) легко доказать, используя правила выполнения соответствующих операций для чисел, представленных алгебраической форме.
1)

2)
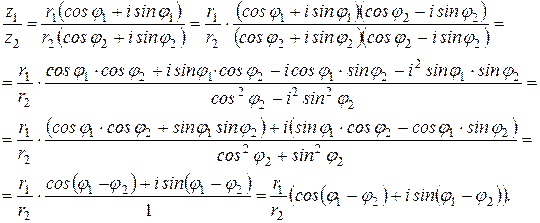
Формула (21) доказывается методом математической индукции. Суть этого алгоритма заключается в следующем: на первом шаге проверяется основание для проведения индукции, т.е. справедливость утверждения при n = 2; на втором шаге выдвигается предположение о справедливости утверждения при n = k; на третьем шаге, с учетом выдвинутого предположения, доказывается справедливость утверждения при n = k + 1.
При доказательстве формулы (21) алгоритм реализуется следующим образом.
1 шаг. При  , используя формулу (19), получаем:
, используя формулу (19), получаем:
 ,
,
т.е. формула (21) остается верной.
2 шаг. Предположим, что формула верна при  , т.е.
, т.е.
 .
.
3 шаг. При 

т.е. формула сохраняет свой вид, следовательно, утверждение – верно.
Пример 6. Если 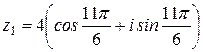 ,
,  , то
, то



Следствие 1. Если  , где
, где  , то
, то
1)  ; (22)
; (22)
2)  ; (24)
; (24)
3)  ; (25)
; (25)
4)  ; (26)
; (26)
5)  ; (27)
; (27)
6) 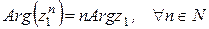 . (28)
. (28)
Очевидно, что равенства (26) – (28) следует рассматривать с точки зрения равенства множеств или с точностью до  . Формулы (22) и (24) с помощью метода математической индукции можно обобщить для любого числа множителей и делителей. Из (21) следует еще одна интересная формула, называемая формулой Муавра.
. Формулы (22) и (24) с помощью метода математической индукции можно обобщить для любого числа множителей и делителей. Из (21) следует еще одна интересная формула, называемая формулой Муавра.
Следствие 2 (формула Муавра)
 . (29)
. (29)
Определение 10. Корнем n-й степени из комплексного числа z называется число  , такое что
, такое что 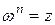 .
.
Обозначение: 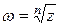 .
.
Теорема 5. Для любого комплексного числа z 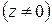 , представленного в тригонометрической форме
, представленного в тригонометрической форме  , где
, где  , существует ровно n корней n -й степени, которые могут быть определены по формуле:
, существует ровно n корней n -й степени, которые могут быть определены по формуле:
 , (30)
, (30)
где  - арифметическое значение корня, к последовательно принимает значения
- арифметическое значение корня, к последовательно принимает значения  .
.
Доказательство. Пусть число  является корнем n -й степени из числа z и в тригонометрической форме имеет вид:
является корнем n -й степени из числа z и в тригонометрической форме имеет вид:  , где
, где 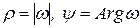 . Тогда,
. Тогда,  .
.
Так как 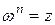 , получаем, что
, получаем, что 
Откуда следует, что  , причем корень понимается в арифметическом смысле – как неотрицательное действительное число, так как по определению модуля комплексного числа
, причем корень понимается в арифметическом смысле – как неотрицательное действительное число, так как по определению модуля комплексного числа  ;
;  .
.
Представив  в виде
в виде  ; нетрудно заметить, что, при
; нетрудно заметить, что, при  , получаются различные комплексные числа, которые для удобства обозначим
, получаются различные комплексные числа, которые для удобства обозначим  (в соответствии с выбираемым значением к).
(в соответствии с выбираемым значением к).
 ;
;
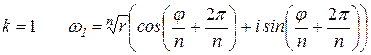 ; ….,
; ….,
 .
.
Числа, получающиеся при остальных значениях к, будут совпадать с одним из уже полученных чисел  , так аргументы этих чисел будут отличаться от аргументов выписанных чисел на число, кратное
, так аргументы этих чисел будут отличаться от аргументов выписанных чисел на число, кратное  . В частности,
. В частности,
 .
.
Самостоятельно проверьте, 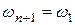 ,
,  .
.
В общем случае, при 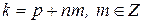 имеем:
имеем:

Что и является доказательством данного утверждения. Теорема доказана.
Замечание. Из последней фразы доказательства теоремы 5 видно, что при использовании формулы (30) вместо набора  можно брать любой набор из n подряд расположенных целых чисел. Например,
можно брать любой набор из n подряд расположенных целых чисел. Например,  или
или  .
.
На комплексной плоскости корни n -й степени из комплексного числа  , где
, где  , располагаются в вершинах правильного n-угольника, вписанного в окружность радиуса
, располагаются в вершинах правильного n-угольника, вписанного в окружность радиуса  , с центром в начале координат, угол поворота от одного числа к другому равен
, с центром в начале координат, угол поворота от одного числа к другому равен  .
.
Пример 7. Найти и изобразить на комплексной плоскости 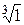 .
.
Решение. Число  . Для перехода к тригонометрической форме воспользуемся геометрическим методом. Построив вектор
. Для перехода к тригонометрической форме воспользуемся геометрическим методом. Построив вектор  (рисунок 9), нетрудно заметить, что
(рисунок 9), нетрудно заметить, что 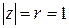 , главное значение аргумента
, главное значение аргумента  .
.


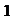

Рисунок 9 – Геометрическая интерпретация Рисунок 10 –Расположение корней числа 1
Следовательно,  . Применяя формулу (30), получаем:
. Применяя формулу (30), получаем:
 ,
,  , т.е.
, т.е.


На комплексной плоскости данные числа располагаются в вершинах правильного треугольника, вписанного в окружность радиуса 1 (рисунок 10).
Помимо тригонометрической формы записи в некоторых приложениях используется показательная форма записи комплексного числа, которая основа на использовании формулы Эйлера:
 . (31)
. (31)
Число  , где
, где  , в этом случае может быть представлено так:
, в этом случае может быть представлено так:
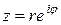 , (32)
, (32)
это и есть показательная форма записи комплексного числа z.
Правила выполнения операций умножения, деления, возведения в степень и извлечения корня в этом случае приобретают вид.
Теорема 6. Если  , то
, то
1)  ;
;
2) 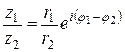 ;
;
3)  ;
;
4) 
Существует также матричное представление комплексных чисел. С этой интерпретацией можно ознакомиться по математической энциклопедии.
Дата добавления: 2015-07-12; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Общегеографические карты. | | | I. ТИПОЛОГИЧЕСКАЯ ПРИНАДЛЕЖНОСТЬ ПАМЯТНИКА |