Логика высказываний

Математическая логика

Логика высказываний

Высказывание – повествовательное предложение (утверждение, суждение), о котором имеет смысл говорить, что оно истинно или ложно.

Высказывание называется простым (элементарным), если его можно рассматривать как некоторое неделимое целое, не содержащее логических связок.

Сложным (составным) называется высказывание, составленное из простых с помощью логических операций.

Конъюнкцией (логическим произведением) двух высказываний P и Q называется высказывание истинное, когда оба высказывания истинны, и ложное во всех других случаях. Обозначения: PÙQ, P&Q, P×Q.

Дизъюнкцией (логической суммой) двух высказываний P и Q называется высказывание ложное в случае, когда оба высказывания ложны, и истинное во всех других случаях. Обозначения: PÚQ, P+Q.

Отрицанием (инверсией) высказывания P называется высказывание истинное, когда высказывание P ложно, и ложное в противном случае. Обозначения: 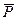, ùP.

Импликацией (логическим следованием) двух высказываний P и Q называется высказывание ложное когда P истинно, а Q – ложно; во всех других случаях высказывание истинно. Обозначения: P®Q.

Эквиваленцией (равнозначностью) двух высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначения: P~Q, PºQ, P«Q.

Неравнозначностью (исключающим «или», сложением по модулю 2) двух высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q не совпадают, и ложное в противном случае. Обозначения: PÅQ, PÎQ.

Алфавит логики высказываний составляют буквы, обозначающие высказывания, логические операции и скобки.

Формула алгебры высказываний определяется следующим образом:

1. Любая переменная, обозначающая высказывание – формула.

Если A и B формула, то (AÙB), (AÚB), (ùA),(A®B) – формулы.

2. Других формул нет.

Подформулой формулы А является ее любая часть, которая сама является формулой.

Каждая формула может интерпретироваться как функция, определенная на множестве {и,л}, со значениями в этом же множестве, полученная из ù,Ù,Ú,® по правилам построения данной формулы. Такую функцию называют также таблицей истинности данной формулы.

Дата добавления: 2015-07-11