Побудова функції щільності розподілу параметру Тнв.

Побудову функції щільності розподілу параметру Т_нв будемо проводити, виходячи з передумови, що цей параметр має нормальний закон розподілу.

3.1. Обчислення статистичних оцінок параметру.

3.1.1. Середнє значення :

3.1.2. Математичне очікування M[Т_нв]:

.

3.1.3. Дисперсія D[Т_нв]:

3.1.4. Середнє квадратичне відхилення :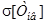

3.1.5. Коефіцієнт варіації (коваріація) :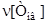

.

3.2. Побудова емпіричної функції щільності розподілу параметру Т_нв.

3.2.1. Основні відомості про функцію щільності розподілу

При вивченні властивостей параметру Т_нв важливою прикладною задачею є визначення імовірності P(Т_нв,k< Т_нв < Т_нв,r) того, що деяке його довільне значення потрапить у певний інтервал DТ_нв = [Т_нв,k; Т_нв,r], (Т_нв,k < Т_нв,r), з діапазону D_Тнв зміни її значень. Використовуючи для розв’язку цієї задачі визначену зарані функцію розподілу F(Т_нв), можна записати:

.

Середня величина імовірності влучання значення Т_нв в інтервал DТ_нв = [Т_нв,k; Т_нв,r] складає:

За умови зменшення значення DТ_нв границею вказаного вище виразу є похідна від функції розподілу F(Т_нв) і називається щільністю розподілу f(Т_нв) випадкової величини Т_нв. Графік функції 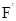(Т_нв) = f(Т_нв) називається графіком функції щільності розподілу. Якщо вид функції f(Т_нв) відомий, то можна визначити імовірність того, що деяке значення Т_нв параметру Т_нв буде знаходитися в певному інтервалі [а;b] з діапазону D_Тнв зміни її значень з імовірністю

P(a < Т_нв < b) = .

Геометрично дану імовірність можна подати як площу фігури, яка утворюється кривою f(Т_нв), ординатами, проведеними з точок а і b і віссю Т_нв. Площа, що знаходиться під усією кривою функції f(Т_нв) щільності розподілу в рамках визначеного діапазону D_Тнв зміни значень параметру Т_нв, дорівнює одиниці.

3.2.2. Побудова графіку функції щільності розподілу для нормального закону

Якщо параметр Т_нв має нормальний розподіл з параметрами М[Т_нв] і σ[Т_нв], то його функція щільності розподілу f(Т_нв) має такий вид (для спрощення виразу М[Т_нв] і σ[Т_нв] замінено на М та σ):

.

f(Т_нв)

Графік такої функції показано на рис.3.

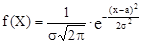Рис.3. Вид функції щільності розподілу для нормального закону

Таким чином, нормальний розподіл визначається двома параметрами: М і σ. Цими параметрами є: М[Т_нв] – математичне очікування параметру Т_нв та σ[Т_нв] – його середнє квадратичне відхилення. Досить знати ці параметри, щоб задати нормальний розподіл. Для побудови графіку f(Т_нв) необхідно скористатись тими результатами, які були отримані на етапі обчислення статистичних оцінок параметру, який досліджується.

Таким чином, зміст домашнього завдання повинен включати:

1. Формулювання мети дослідження.

2. Початкові дані відповідно призначеного варіанту (дані будуть викладені нижче).

3. Ранжовану за зростанням значень елементів вибірку, результати визначення діапазону D_Тнв та поділу його на ділянки із встановленням меж їх значень.

4. Результати побудови частотного та кумулятивного ряду розподілу значень параметру Т_нв, відповідних гістограм та функції розподілу F(Т_нв).

5. Результати обчислення значень статистичних оцінок (середнього, математичного очікування, дисперсії, середнього квадратичного відхилення, коваріації) параметру Т_нв.

6. Результати побудови графіка функції щільності розподілу f(Т_нв) за нормальним законом.

7. Сформувати висновки за проведеними дослідженнями щодо обґрунтувати термінів міжремонтного та гарантійного ресурсів даного ТП.

Дата добавления: 2015-07-11