
Читайте также:
|
I. Проверить, коммутируют ли приведенные ниже операторы?
1. 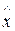 и
и 
2.  и
и 
3. 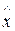 и
и 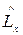 , где
, где 
4. 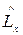 и
и 
5. 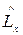 и
и 
II. Найти операторы, сопряженные с приведенными ниже. Определить какие операторы являются эрмитовыми.
1. 
2. 
3. 
4. 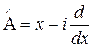
5. 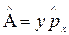
III. Доказать:
1. если операторы 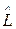 и
и  эрмитовы и коммутируют, то оператор
эрмитовы и коммутируют, то оператор 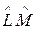 также эрмитов;
также эрмитов;
2. если операторы 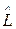 и
и  эрмитовы и некоммутирующие, то оператор
эрмитовы и некоммутирующие, то оператор  эрмитов;
эрмитов;
3. если операторы 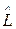 и
и  эрмитовы и некоммутирующие, то оператор
эрмитовы и некоммутирующие, то оператор  эрмитов;
эрмитов;
4. если операторы 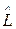 и
и  эрмитовы и некоммутирующие, то оператор
эрмитовы и некоммутирующие, то оператор  не эрмитов;
не эрмитов;
5. если оператор 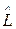 линейный, то оператор
линейный, то оператор  эрмитов;
эрмитов;
IV. 1. Найти собственные функции и собственные значения оператора  , если
, если  , где
, где  – постоянная величина.
– постоянная величина.
2. Найти собственные функции и собственные значения оператора  (Оператор задан в сферических координатах).
(Оператор задан в сферических координатах).
3. Найти собственные функции и собственные значения оператора  (Оператор задан в сферических координатах).
(Оператор задан в сферических координатах).
4. Найти собственные функции и собственные значения оператора  , если
, если  .
.
5. Найти собственные функции и собственные значения оператора 
V. 1. Вычислить среднее значение  для одномерного гармонического осциллятора, состояние которого описывается функцией
для одномерного гармонического осциллятора, состояние которого описывается функцией 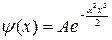 , где
, где 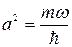 .
.
2. Вычислить среднее значение кинетической энергии  линейного гармонического осциллятора, если состояние его описывается функцией
линейного гармонического осциллятора, если состояние его описывается функцией  , где
, где 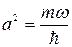 .
.
3. Волновая функция состояния частицы имеет вид  , где
, где  - вещественная функция. Найти средний импульс частицы в этом состоянии.
- вещественная функция. Найти средний импульс частицы в этом состоянии.
4. В некоторый момент времени частица находится в состоянии 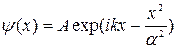 , где
, где  и
и  - постоянные. Найти среднее значение ее координаты
- постоянные. Найти среднее значение ее координаты  .
.
5. Найти среднее значение физической величины, представляемой оператором  , если состояние частицы описывается функцией
, если состояние частицы описывается функцией 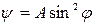 .
.
VI. Определить возможные значения физической величины, представляемой оператором  и их вероятности для системы, находящейся в состоянии:
и их вероятности для системы, находящейся в состоянии:
1. 
2. 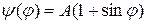
3. 
4. 
5. 
(Оператор задан в сферических координатах)
Литература
1. Дирак П. Принципы квантовой механики.–М: Наука, 1979.
2. Вакарчук І. О. Квантова механіка: Підручник.– Львів: ЛДУ ім.. І. Франка, 1998.
3. Блохинцев Д.И. Основы квантовой механики. М.: Наука, 1983.
4. Давыдов А.С. Квантовая механика. М.: Наука, 1973.
5. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М.: Наука, 1989.
6. Юхновський І.К. Квантова механіка. Київ: Либідь, 1995.
7. Федорченко А.М. Теоретична фізика. Київ: Вища школа, 1993, т. 2.
8. Фок В.А. Начала квантовой механики. М.: Наука, 1976.
9. Шифф Л. Квантовая механика. М.: Из-во иностр. лит., 1959.
10. Мессиа А. Квантовая механика: в 2-х томах, М.: Наука, 1978, т. 1.
11. Иродов И.Е. Задачи по квантовой физике. М.: «Высшая школа», 1991.
12. Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой механике. М.: Наука, 1981.
13. Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.
14. Рихтмайер Р. Принципы современной математической физики, М.:1982.
[1] Бор.М. Атомная физика. – М.: Мир, 1965, с 119
[2] Об обобщенных функциях см. Гельфанд И.М., Шилов Г.Е. Обобщенные функции. М., 1958
Дата добавления: 2015-07-11; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Упражнения. | | | Начало работы |