Парциальные частоты колебаний

Парциальной называется частота колебаний колебательной системы, у которой все степени свободы, кроме одной, ограни­чены. Следовательно, любая сложная колебательная система, об­ладающая многими степенями свободы, будет колебаться с пар­циальной частотой, если ей предоставить одну степень свободы при ограничении всех остальных степеней свободы.

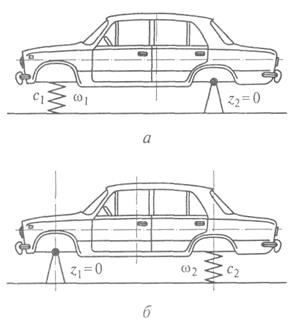
На рис. 13.6 приведены схемы, иллюстрирующие колебания подрессоренной массы с парциальными частотами ω₁ и ω₂.

Если подрессоренная масса закреплена так, что перемещения z ₂ = 0, то она имеет одну степень свободы и парциальная частота колебаний подрессоренной массы равна ω₁.

При ограничении перемещения подрессоренной массы так, что z ₁ = 0, частота ее колебаний будет парциальной и равной ω₂.

Как видно из рис. 13.6, парциальные частоты можно получить для любой колебательной системы, если ограничивать перемеще­ния масс таким образом, чтобы колебательная система обладала только одной степенью свободы.

Свободные колебания передней и задней частей кузова авто­мобиля, как видно из уравнений свободных колебаний, связаны между собой и происходят с частотами, отличающимися от пар­циальных — ω₁и ω₂. Эти часто­ты свободных колебаний назы­ваются частотами связи, или собственными частотами коле­баний.

Исследованиями установле­но, что свободные колебания подрессоренной массы автомо-

Рис. 13.6. Схемы, иллюстрирующие колебания подрессоренной массы автомобиля с парциальными час­тотами при ограничении перемеще­ния задней (а) и передней (б) час­тей его кузова

биля совершаются одновременно с высокой и низкой частотами. При этом движение любой точки кузо­ва автомобиля представляет собой негармоническое колебание, выз­ванное взаимным наложением двух гармонических колебаний высокой и низкой частоты.

Рис. 13.7. Колебательная система автомобиля без затухания и не-подрессоренных масс при ε _у = 1

При коэффициенте распределе­ния подрессоренных масс ε _у = 1 связь между колебаниями передней и задней частей кузова отсутствует (рис. 13.7). В такой колебательной системе приведенные массы М ₁и М ₂соединены между собой шарнирно жестким невесомым стержнем, расположены на расстоя­ниях l ₁ и l ₂ от центра тяжести кузова автомобиля и имеют следую­щие значения:

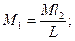
Приведенные массы М ₁и М ₂соответствуют весу кузова, при­ходящемуся соответственно на передние и задние колеса при не­подвижном автомобиле.

В этом случае система уравнений, описывающих свободные колебания автомобиля, распадается на два независимых уравне­ния.

Уравнение свободных колебаний передней части кузова авто­мобиля имеет следующий вид:

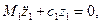
а уравнение свободных колебаний задней части кузова записыва­ется в виде

При этом передняя и задняя части кузова будут совершать сво­бодные гармонические колебания соответственно с парциальны­ми частотами

Частота колебаний, мин^–1, передней и задней частей кузова автомобиля в этом случае

где f ₁ и f ₂ – статический прогиб упругих устройств передней и задней подвесок автомобиля, см.

У легковых автомобилей взаимная связь между колебаниями передней и задней частей кузова незначительна. Исследования показали, что колебания передней и задней частей кузова авто­мобиля можно считать практически независимыми, когда коэф­фициент распределения подрессоренных масс ε _у = 0,8... 1,1. Этому условию удовлетворяют только легковые автомобили.

Дата добавления: 2015-07-10