|
Читайте также: |
Свободными называются колебания, совершаемые автомобилем на дороге с ровной поверхностью после проезда неровностей.
Для изучения свободных колебаний автомобиля в продольной вертикальной плоскости его подрессоренную массу заменим тремя приведенными массами, которые соединены между собой невесомым жестким стержнем. При этом не будем учитывать влияния затухания (амортизаторов) и неподрессоренных масс (мостов, колес). Колебательная система автомобиля, соответствующая принятым допущениям, приведена на рис. 13.5.
|
В указанной колебательной системе М 1, М 2и М 3 — приведенные подрессоренные массы. М 1и М 2расположены на расстояниях l 1и l 2 от центра тяжести кузова автомобиля, а M 3 – в центре тяжести; с 1 и с 2 — приведенные жесткости передней и задней подвесок.
Для того чтобы эта трехмассовая колебательная система соответствовала в динамическом отношении действительной системе, необходимо выполнение следующих условий:
Рис. 13.5. Колебательная система автомобиля без затухания и неподрессоренных масс:
а — подвеска подрессоренной массы (кузова); б — схема системы; ЦТ — центр тяжести
• сумма всех трех масс должна быть равна подрессоренной массе автомобиля (М 1 + М 2 + М 3 = М);
• центр тяжести трехмассовой колебательной системы должен
совпадать с центром тяжести подрессоренной массы автомобиля
(М 1 l 1 = М 2 l 2);
• моменты инерции трехмассовой колебательной системы и
подрессоренной массы автомобиля относительно поперечной оси
у, проходящей через центр тяжести, должны быть равны (М 1 l 1 +
+ М 2 l 2 = M ρ у 2, = J);где ρ у — радиус инерции подрессоренной массы
автомобиля относительно поперечной оси у, проходящей через
центр тяжести.
Решим совместно указанные выше уравнения и определим значения приведенных масс М 1, М 2и М 3.
С этой целью поочередно подставим значения М 1и М 2из второго уравнения в третье и найдем массы М 1и М 2. Затем найденные значения М 1и М 2подставим в первое уравнение и определим массу М 3.
В результате получим значения приведенных масс:
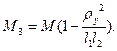
Отношение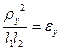 
называется коэффициентом распределе-
ния подрессоренных масс автомобиля. Он определяет наличие связи
между колебаниями передней и задней частей кузова автомобиля. Так, при ε у = 1 связь между колебаниями передней и задней частей кузова отсутствует.
Свободные колебания подрессоренной массы автомобиля можно описать следующей системой уравнений:
Разделив уравнения соответственно на М 1и М 2,получим
или
где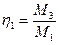 
и 
— коэффициенты связи между колебани-
ями передней и задней частей кузова; 
и 
— пар-
циальные, или частные, частоты свободных колебаний.
Дата добавления: 2015-07-10; просмотров: 186 | Нарушение авторских прав