Краткие теоретические сведения. Комплексной функцией цепи называется отношение комплексной амплитуды реакции к

Комплексной функцией цепи называется отношение комплексной амплитуды реакции к комплексной амплитуде воздействия в установившемся гармоническом режиме:

. (2.1)

Так как комплексное действующее значение (комплекс) отличается от комплексной амплитуды множителем 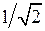, можно дать равносильное (2.1) определение:

. (2.2)

Комплексные функции могут характеризовать двухполюсник или четырехполюсник. Для двухполюсника воздействие и реакция рассматриваются на одной паре полюсов (рис.2.1). Поэтому возможны две комплексные функции двухполюсника. Это входное комплексное сопротивление

и входная комплексная проводимость

.

Эти функции называются входными.

Рис.2.2. К определению передаточных функций

Для четырехполюсника воздействие приложено к входным зажимам, а реакция рассматривается на выходных зажимах (рис.2.2). Так как воздействие может быть задано в виде либо напряжения на входе, либо входного тока, а реакцией может быть либо напряжение на выходе, либо выходной ток, то возможны четыре комплексные функции четырехполюсника, называемые передаточными. Для случая, показанного на рис.2.2,а, это комплексный коэффициент передачи напряжения

и комплексная передаточная проводимость

.

Для случая, показанного на рис.2.2,б, передаточными функциями являются комплексное передаточное сопротивление

и комплексный коэффициент передачи тока

.

Применяя общее обозначение комплексной функции цепи , можно записать

,

где называется амплитудно-частотной характеристикой (АЧХ),

а называется фазо-частотной характеристикой (ФЧХ) цепи.

Из определения комплексной функции (2.1) следует, что АЧХ имеет смысл зависимости отношения амплитуд реакции и воздействия от частоты воздействия. ФЧХ есть зависимость сдвига фаз между реакцией и воздействием от частоты воздействия.

В настоящей лабораторной работе исследуются комплексные коэффициенты передачи четырехполюсников Г-образной структуры (рис.2.3). Предполагается, что нагрузка отсутствует. Так как через ветви и протекает один и тот же ток , напряжения на выходе и входе четырехполюсника выражаются следующим образом:

, .

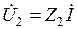Отсюда:

. (2.3)

Покажем применение этого соотношения для нахождения частотных характеристик четырехполюсника, схема которого приведена на рис.2.4. В данном случае:

, .

Подставляя эти выражения в формулу (2.3), получим

.

Введем обозначения:

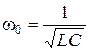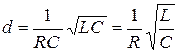, . (2.4)

Тогда выражение передаточной функции приводится к виду

. (2.5)

Взяв модуль дроби в этом выражении, получаем АЧХ

. (2.6)

Особенность вычисления аргумента выражения (2.5) заключается в том, что вещественная часть знаменателя дроби при изменении частоты меняет знак, что приводит к составному выражению ФЧХ. В данном случае можно упростить запись ФЧХ, предварительно умножив числитель и знаменатель дроби на - j:

.

Теперь вещественные части числителя и знаменателя неотрицательны, и можно записать ФЧХ в виде

. (2.7)

Заметим, что численные расчеты по формулам (2.6) - (2.7) производить неудобно. Упрощения численных расчетов можно добиться, введя нормированную частоту

.

Разделив числитель и знаменатель в (2.5) на , получим

.

Теперь формулы (2.6) и (2.7) приобретают значительно более простой вид:

, (2.8)

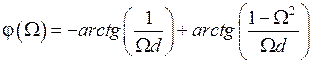. (2.9)

Методика расчета частотных характеристик по формулам (2.8) - (2.9) сводится к следующему. Сначала для выбранного значения частоты f (или ) вычисляется нормированная частота , затем производятся вычисления формулам (2.8) - (2.9). Далее эта процедура повторяется для других частот генератора.

К теоретическому и экспериментальному исследованию в настоящей лабораторной работе предлагается шесть цепей. Это три двухэлементных четырехполюсника (рис.2.6) и три трехэлементных четырехполюсника (рис.2.7). Каждая бригада исследует две цепи. Номера исследуемых цепей для каждой бригады приведены в табл.2.1. Значения параметров R, L, C и формулы передаточных функций цепей приведены в табл. 2.2 и 2.3.

Таблица 2.1. Номера исследуемых цепей (см. рис.2.6 и 2.7)

Бригады
Номера цепей	1 и 4	2 и 5	3 и 6

Рис.2.6. Двухэлементные четырехполюсники для исследования  

Рис.2.7. Трехэлементные четырехполюсники для исследования  

Таблица 2.2. Параметры и передаточные функции двухэлементных цепей

Номер цепи	Схема	Параметры	Передаточная функция	Обозначения
		R = 430 Ом С = 67 нФ
		R = 1 кОм L = 15 мГн
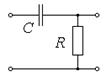
		R = 620 Ом С = 5,6 нФ

Таблица 2.3. Параметры и передаточные функции трехэлементных цепей

Дата добавления: 2015-09-04