Статическое и полное конструктивное уравновешивание ротора

Выполнил(и): студент(ы)__________________

__________________

__________________

__________________

группа__________________

Руководитель:

преподаватель__________________

Отметка о зачете:

__________________________________

дата

20____/ ____ учебный год

Цель работы:

1. Исходные данные:

Плоскость
Величина неуравновешенной массы, г.
Расстояние от оси вращения ротора, мм.
Угол, составленный радиус - вектором массы с положительным направлением оси Х, град.

Схема установки и расположения неуравновешенных масс

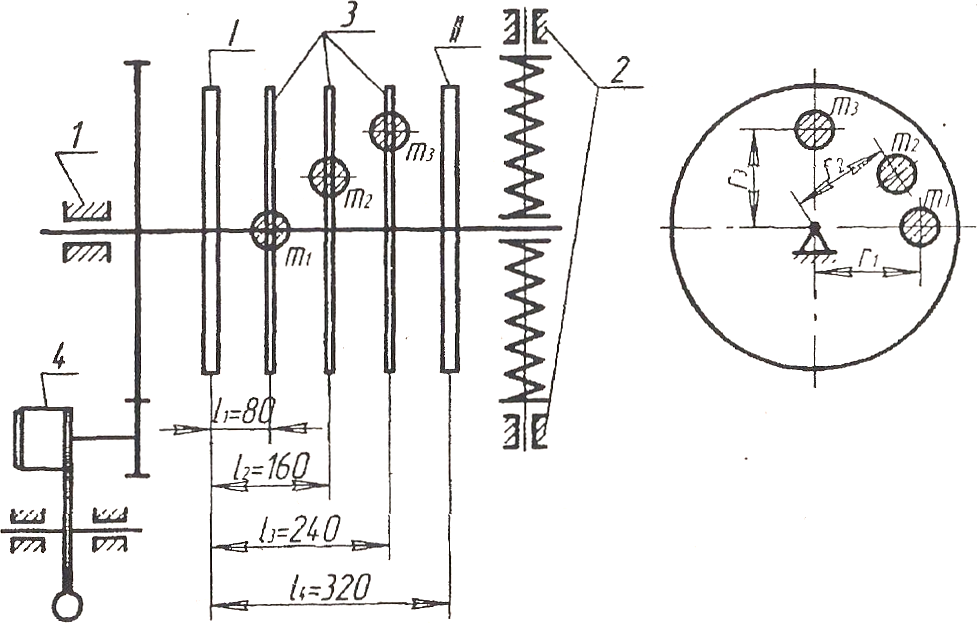
1 –

2 –

3 –

4 –

2. Статическое уравновешивание.

m₁r₁ = m₂r₂ = m₃r₃ =

3. Многоугольник статических дисбалансов ротора:

μ =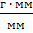

4. Параметры противовеса:

m_n = r_n = α_n =

Противовес установить либо в плоскости 1, либо в плоскости 2.

5. Полное уравновешивание.

а) Динамическое уравновешивание:

m₁r₁l₁ = m₂r₂ l₂ = m₃r₃ l₃ =

Многоугольник динамических дисбалансов ротора

μ =

Параметры противовеса в плоскости 11:

r ₁₁ = m ₁₁ = α ₁₁ =

б) статическое уравновешивание:

m₁r₁ = m₃r₃ =

m₂r₂ = m₁₁ r₁₁=

Многоугольник статических дисбалансов ротора:

μ =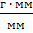

Параметры противовеса в плоскости 1:

m₁ =

r₁ =

α₁ =

Вывод:

Контрольные вопросы

1. Что является причиной неуравновешенности ротора?

2. Какие виды неуравновешенности ротора вы знаете?

3. Условие статической уравновешенности ротора.

4. Условие динамической уравновешенности ротора.

5. Условие полной уравновешенности ротора.

6. Что такое статический дисбаланс?

7. Что такое динамический дисбаланс?

8. Указать минимум противовесов, необходимых для статического уравновешивания ротора.

9. Указать минимум противовесов, необходимых для полного уравновешивания ротора.

---

Дата добавления: 2015-09-04