Общие сведения. Принцип наименьшего сопротивления сформулирован С.И

Принцип наименьшего сопротивления сформулирован С.И. Губкиным следующим образом: «В случае возможности перемещения точек деформируемого тела в различных направлениях каждая точка тела перемещается в направлении наименьшего сопротивления» [5].

Из принципа следует, что наибольшая деформация произойдет в направлении наименьшего сопротивления.

В случае одинаковых внешних условий по двум возможным направлениям перемещения точки логично предположить, что направление наименьшего сопротивления будет являться направлением кратчайшей нормали, проходящей через данную точку к периметру сечения. Многочисленные опытные данные подтверждают это положение.

Рассмотрим формоизменение прямоугольного параллелепипеда в плоских бойках.

Пусть деформируемый образец имеет в определенный момент деформации размеры, указанные на рис. 1. Дадим образцу осадку на величину dh. При этом размеры образца в плане увеличатся на величину db и dl. На основании принципа наименьшего сопротивления биссектрисы АВ, АС и прямая АD будут линиями раздела течения металла в различных направлениях (указано стрелками). Поскольку приращение 0,5 dl произойдет за счет смещенного по высоте объема призмы с основанием АВС, то можно записать из условия постоянства объема треугольной призмы

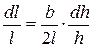, или . (1)

Условие постоянства объема для прямоугольного параллелепипеда запишется:

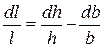, или . (2)

Решая совместно уравнения (1) и (2), получим:

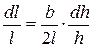и . (3)

Уравнения (3) показывают, что поперечная и продольная деформации образца зависят от соотношения размеров образца в плане и от величины относительной деформации по высоте.

Дата добавления: 2015-09-01