
|
Читайте также: |
> with(plottools):
> ss:=plot(Y,x=0..28000,color=blue,thickness=3):
ss1:=plot(Y1,x=0..28000,color=blue,thickness=3):
ss2:=plot(Y2,x=0..28000,color=blue,thickness=3):
ss3:=plot(Y3,x=0..28000,color=blue,thickness=3):
ss4:=plot(Y4,x=0..28000,color=blue,thickness=3):
# ss, ss1, ss2, ss3, ss4 - графические структуры траектории полета снаряда
ll:=line([-450,0],[-450,1900],color=black,thickness=15):
ll1:=line([0,1900],[0,2200],color=blue,thickness=15):
> with(plots):
> display([ss,ss1,ss2,ss3,ss4,ll,ll1],
title=`Траектория полета снаряда`,
titlefont=[TIMES,ROMAN,14],
labels=["Дальность полета"," Высота подъема "],
labeldirections=[HORIZONTAL,VERTICAL],
labelfont=[TIMES,ROMAN,14],
view=[-500..28000,0..16000]);
Warning, the names arrow and changecoords have been redefined

Выясним можно ли попасть в цель при V o = 500 м/c и h = 2 км, расположенную на расстоянии s = 25 км от уступа. Для этого из уравнения траектории используя данные условия найдем 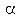 .
.
> restart;
> Y:=-1/2*(-2*h*Vo^2*cos(alpha)^2-2*sin(alpha)*x*Vo^2*cos(alpha)+g*x^2)/Vo^2/cos(alpha)^2:
> Alpha:=solve(Y,alpha);

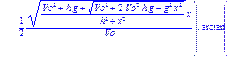
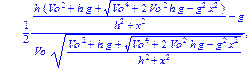
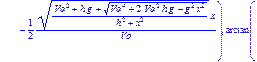


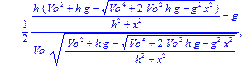
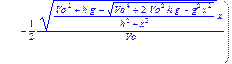
Решив квадратное уравнение, мы получили формулу для вычисления угла Alpha. Теперь подставим начальные условия и найдем численное значение угла (в радианах и сразу переведем в градусы).
Дата добавления: 2015-09-04; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задаваемые параметры (вСИ). | | | нұсқа |