Читайте также:
|
Поток вектора напряженности электрического поля в вакууме сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную.
.
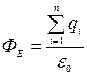Если внутри сферы зарядов нет, то поток равен нулю.
Теорема Остроградского-Гаусса позволяет сравнительно просто рассчитывать электрические поля при симметрично распределенных зарядах.
1. Поле равномерно заряженной сферической поверхности.
Сферическая поверхность радиуса R с общим зарядом Q заряжена с поверхностной плотностью s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис.). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r > R, то внутрь поверхности попадает весь заряд, создающий рассматриваемое поле, и по теореме Остроградского-Гаусса
,
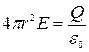откуда
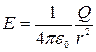, при r ³ R
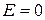, при r < R.
Разность потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от центра сферы (r1 > R, r2 > R, r2 > r1), равна
.
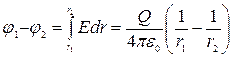Потенциал поля вне сферической поверхности
.
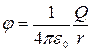Дата добавления: 2015-09-04; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема Остроградского-Гаусса позволяет определить поток вектора , создаваемого системой зарядов. | | | Внутри сферической поверхности |