
Читайте также:
|


Доведення (метод математичної індукції):
База індукції: n=1 – очевидна, n=2 – 
Індукційний крок: Припустимо, що формула виконується для n. Доведемо, що тоді вона виконується і для n+1.


звідки:

Перший i третiй доданки у правiй частинi є кiлькостями елементiв в об’єднаннях множин, кiлькiсть яких дорiвнює n i до них можна застосувати припущення iндукцiї:
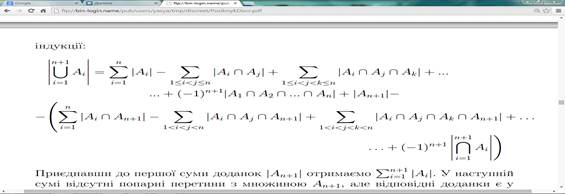



Таким чином, об’єднавши вiдповiднi суми остаточно отримуємо:

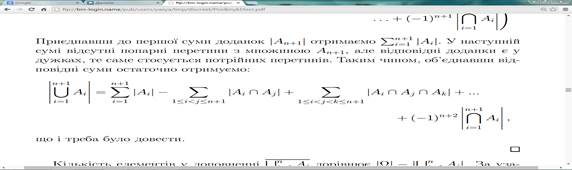
що і треба було довести.
21. Класична ймовірність
Нехай Ω – деяка скінченна множина елементарних (найпростiших) подiй. Будь-яку пiдмножину A ⊆ Ω будемо називати подiєю.
Класичною ймовiрнiстю подiї A називається число:

Властивостi класичної ймовiрностi (наступнi властивостi легко отримати безпосередньо з означення):

Дата добавления: 2015-09-04; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Декартiв добуток множин. | | | Очень приятно, Дита фон Тиз |