на основе численных методов

Контрольная точка №2

Определение нестационарных температурных полей

на основе численных методов

14.2.1. Записать конечно-разностное уравнение нестационарной
теплопроводности для первого, среднего и последнего реального слоя пластины, мысленно разделенной на (2 N ₁+3)+ k слоев равной толщины при дискретизации пространства методом элементарного
теплового баланса (МЭТБ) или методом сеток (методом конечных разностей МКР) (рис. 14.10, 14.11).

Число k и вид дискретизации пространства выбрать из табл. 14.2 по цифре N ₁, а по цифре N ₂ выбрать из этой таблицы номер п
предшествующего временного слоя длительностью 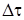и явную или неявную схему счета.

Таблица 14.2

Данные к численному расчету нестационарной теплопроводности в пластине

N 1	k	Схема расчета по методу	N 2	п	Схема счета
		МЭТБ			Явная
		МКР			Неявная
		МЭТБ			Явная
		МКР			Неявная
		МЭТБ			Явная
		МКР			Неявная
		МЭТБ			Явная
		МКР			Неявная
		МЭТБ			Явная
		МКР			Неявная

14.2.2. Для условий задачи 14.2.1 записать конечно-разностный
аналог граничных условий первого рода (ГУ-I: известны температуры и ), второго рода (ГУ-II: известны плотности теплового потока и ) или третьего рода (ГУ-III: известны температуры омывающих сред 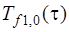, и коэффициенты теплоотдачи , ) на ограничивающих поверхностях пластины.

Таблица 14.3

Данные к численному расчету нестационарной теплопроводности в пластине

N 1	Род граничных условий на левой плоскости	N 2	Род граничных условий на правой плоскости
	ГУ-III		ГУ-III
	ГУ-II		ГУ-II
	ГУ-I		ГУ-I
	ГУ-III		ГУ-III
	ГУ-II		ГУ-II
	ГУ-I		ГУ-I
	ГУ-III		ГУ-III
	ГУ-II		ГУ-II
	ГУ-I		ГУ-I
	ГУ-III		ГУ-III

14.2.3. Записать конечно-разностное уравнение нестационарной
теплопроводности для элементарного прямоугольника с координатами центра i = N ₁ + 2 по оси 0 х и j = N ₂ + 4 по оси 0 у. Cхему счета
(явную или неявную) выбрать по цифре N ₁, а номер предшествующего временного слоя п – по цифре N ₂ (табл. 14.4).

Таблица 14.4

Данные к численному расчету нестационарной теплопроводности
в двухмерной области

N 1	Схема счета	N 2	п
	Явная
	Неявная
	Явная
	Неявная
	Явная
	Неявная
	Явная
	Неявная
	Явная
	Неявная

14.2.4. Используя данные задачи 14.2.3, записать конечно-разностное уравнение нестационарной теплопроводности по методу переменных направлений.

14.2.5. Записать конечно-разностный аналог граничных условий
первого рода (ГУ-I: известны температуры и ), второго рода (ГУ-II: известны плотности теплового потока и ) или третьего рода (ГУ-III: известны температуры омывающих сред 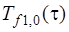, и коэффициенты теплоотдачи , ) на ограничивающей поверхности элементарного прямоугольника. Выбор
координат его центра по осям 0 х и 0 у приведен в табл. 14.5
в зависимости от цифр N ₁ и N ₂. Номер п предшествующего временного слоя определяется по формуле n = N ₁ + N ₂ + k (табл. 14.5).

Таблица 14.5

Данные к численному расчету нестационарной теплопроводности
в двухмерной области

N 1	i	j	N 2	k
		4+ N 1
		8+ N 1
		8+ N 1
		8+ N 1
	6+ N 1
	9+ N 1
	11+ N 1
	11+ N 1
		10+ N 1
		5+ N 1

Рис. 14.11. Дискретизация двухмерной области протекания
процесса нестационарной теплопроводности

Для решения задач 14.2.3 – 14.2.5 использовать результаты пп.1.8 и рис. 14.11.

№ 14.2.1.

1) конечно-разностное уравнение нестационарной теплопроводности для первого слоя, при n=19:

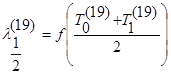
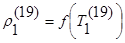
2) конечно-разностное уравнение нестационарной теплопроводности для 11 (середина) слоя, при n=19:

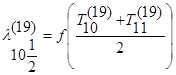
3) конечно-разностное уравнение нестационарной теплопроводности для 21 (последнего) слоя, при n=19:

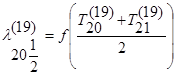
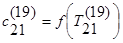
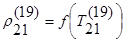
№ 14.2.2.

1) конечно-разностный аналог граничных условий второго рода (ГУ-II) на левой плоскости, при n=19:

2) конечно-разностный аналог граничных условий третьего рода (ГУ-III) на правой плоскости, при n=19:

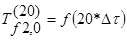
№ 14.2.3.

конечно-разностное уравнение нестационарной теплопроводности для элементарного прямоугольника с координатами центра i =6и j = 10, при n=28:

№ 14.2.4.

конечно-разностное уравнение нестационарной теплопроводности по методу переменных направлений для элементарного прямоугольника с координатами центра i =6и j = 10, при n=28:

по направлению оси Ох:

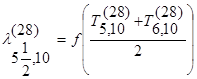
по направлению оси Оy:

№ 14.2.5.

1) конечно-разностный аналог граничных условий первого рода (ГУ-I) для элементарного прямоугольника с координатами центра i =10и j = 2, при n=98:

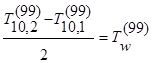
2) конечно-разностный аналог граничных условий второго рода (ГУ-II) для элементарного прямоугольника с координатами центра i =10и j = 2, при n=98:

3) конечно-разностный аналог граничных условий третьего рода (ГУ-III) для элементарного прямоугольника с координатами центра i =10и j = 2, при n=98:

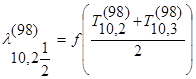
Дата добавления: 2015-09-04