Читайте также:
|
Начальный объем находим из уравнения состояния:
м3.
Показатель политропы находим из уравнения 
:
, откуда n=1.39.
Конечный объем находим по уравнению политропы 
:
м3.
Работу расширения определим по формуле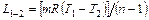 
:
кДж.
Изменение внутренней энергии определяем по средним теплоемкостям, что дает более точный результат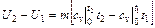 
:
кДж.
Соответственно удельное значение составит: 
кДж/кг.
Количество подведенной теплоты 
;
показатель адиабаты 
;
изменение энтальпии 
;
кДж/кг;
; 
кДж.
Проверяем, выполняется ли первый закон термодинамики для нашего политропного процесса 
:
кДж.
Погрешность в расчете допустима и составляет 0,2 кДж/кг.
Изменение энтропии определяем как 
кДж/(кг·К).
Дата добавления: 2015-09-01; просмотров: 24 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теоретические основы | | | Теоретические основы |