Выполнение работы.

1. Стержни крестовины завинтить до упора, грузы Р закрепить на середине стержней.

2. Взвесит платформу вместе с крючком (). На платформу установит грузик массой .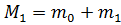

3. Закрепить нить на малом радиусе r шкива. Вращая крестовину против часовой стрелки переместить платформу в верхнее положение зафиксировать маятник нажатием сердечника электромагнита.

4. По шкале h определить ход груза (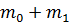), разницу его верхнего и нижнего положений.

5. Нажать на табло миллисекундомера кнопку «сброс», а за тем «пуск»

6. Проверить отсчет времени t хода маятника по миллискундомеру.

7. Повторить 3-6 пункт для грузов

8. Не меняя положения грузов Р, закрепит нить на большом радиусе R шкива.

Расчеты:

= 0,115 кг h = 0,31 м

= 0,170 кг

= 0,225 кг

Малый радиус

№ п/п	r, м	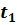, с ()	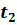, с ()	, с ()
	0,214	6,015	4,226	3,820
		6,388	4,468	3,545
		6,249	4,359	3,545
		6,099	4,452	3,705
		6,066	4,413	3,791

Большой радиус

№ п/п	R, м	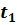, с ()	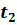, с ()	, с ()
	0,419	2,185	2,085	1,790
		2,750	2,279	1,805
		2,055	2,232	1,907
		2,324	1,950	1,661
		2,145	2,171	1,855

Рассчитать, M, I по формулам:

1. Для малого радиуса:

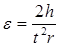
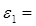0.999 рад/с²

1.73 рад/с²

2.256 рад/с

0.01 Нм

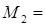0.02 Нм

0.03 Нм

0.01

0.012

0.014

2. Для большого радиуса:

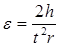
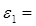1.6 рад/с²

2.7 рад/с²

4.152 рад/с²

0.022 Нм

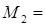0.046 Нм

0.069 Нм

0.015

0.0164

0.0165

График зависимости

Вычислим границы доверительного интервала в определении момента инерции, где - приборные погрешности, - случайная погрешность.

g - цена деления измерительного прибора;

tµ,95 – значение коэффициента Стьюдента.

1.05*10^-3 м

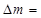0.01 кг

1.05*10^-3 м

0.785 c

0.011

0.015

Для малого радиуса: 0.003

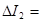0.004

Для большого радиуса: 0.006

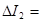0.008

Проверка основного закона динамики для вращательного движения.

Меняя массу груза или радиус шкива, что ведёт к изменению момента силы, при неизменном положении грузов на крестовине, убедиться в том, что угловое ускорение изменяется пропорционально моменту силы, а отношение остаётся постоянным, т.е. момент инерции крестовины не изменяется.

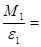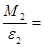0.014 0.014 0.014

Из этого следует то, что основной закон динамики для вращательного движения выполняется.

Вывод: Мы Определили момент инерции маятника Обербека. Также поверили выполнение основного закона динамики для вращательного движения. Для нашего случая основной закон динамики для вращательного движения выполняется. Проверку этого закона мы провели следующим образом: меняя массу груза или радиус шкива, что ведёт к изменению момента силы, при неизменном положении грузов на крестовине, мы убедились в том, что угловое ускорение изменяется пропорционально моменту силы, а отношение остаётся постоянным, т.е. момент инерции крестовины не изменяется.

Контрольные вопросы

1. Дать понятия условной скорости и углового ускорения. Вывести их связь в соответствующими влияниями поступательного движения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

Тангенциальная составляющая ускорения a_τ=dv/dt, v = ωR и

Нормальная составляющая ускорения

Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: s = Rφ, v = Rω, а_τ = Rɛ, a_n = ω²R.

В случае равнопеременного движения точки по окружности (ω=const) ω = ω₀ ± ɛ t, φ = ω₀t ± ɛ t²/2, где ω₀ — начальная угловая скорость.

2. Охарактеризовать понятие момента силы относительно точки и оси, момента инерции.

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Пара сил — система двух сил F1 и F2, действующих на твёрдое тело, равных друг другу по абсолютной величине, параллельных и направленных противоположно друг другу. Пара сил не имеет равнодействующей, то есть её действие на тело не может быть механически эквивалентно действию какой-нибудь одной силы; соответственно пару сил нельзя уравновесить одной силой.

Моментом силы относительно точки О называется вектор , равный векторному произведению , где - радиус-вектор,определяющий положение точки приложения силы относительно точки O.

3. Сформулировать и записать основной закон динамики для вращательного движения.

Основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы , действующий на вращательное тело, равен изменению его момента импульса d L ”:

или = d L.

Дата добавления: 2015-09-01