Читайте также:
|
2.
Для піраміди з вершинами 
, 
обчислити об’єм, площу грані АВС і висоту, опущену на цю грань.
3.
Скласти рівняння бісектрис кутів, утворених двома прямими 
і 
.
4. Знайти область визначення функції 
5. Знайти границю функції.
.
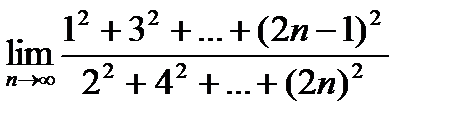6. Знайти границю функції.
.
7. Знайти границю функції.
, (
).
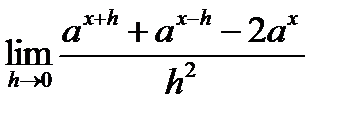Знайти похідну функції:
8. 
9. 
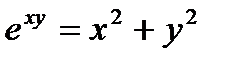
10. 
11. 
12. Вивести формули для сум:
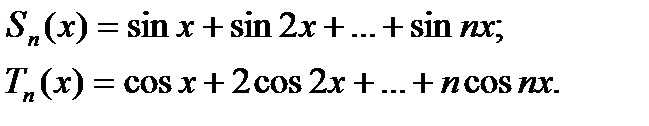
Довести, що якщо функція має в скінченому чи нескінченному інтервалі обмежену похідну, то рівномірно неперервна на.
Дата добавления: 2015-09-02; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дослідити функцію методами диференціального числення і побудувати її графік | | | Довести, що якщо функція диференційована на нескінченному інтервалі і |