Данная методика позволяет с высокой точностью локализовать неисправность и не требует высокой квалификации обслуживающего персонала.

Во многих случаях для микропроцессорной аппаратуры и микроЭВМ не удается применить автоматическое диагностирование на основе встроенных или внешних тестовых средств диагностирования или их комбинаций из-за ее сложности и высокой стоимости. Тогда следует позаботиться об облегчении ручного обслуживания, в том числе ручного поиска неисправностей, с тем чтобы эту работу мог выполнять персонал невысокой квалификации.

Существенной проблемой при ручном обслуживании является сжатие информации о правильных (эталонных) и наблюдаемых при контроле реакциях аппаратуры на тестовые последовательности.

Необходимость сжатия двоичных последовательностей (векторов) произвольной длины диктуется тем, что coвременная микропроцессорная техника использует достаточно сложные функциональные узлы, которые требуют для диагностирования ввода большого числа тестовых. векторов, с тем чтобы обеспечивалась проверка всех возможных состоянии устройства.

Сжатие информации облегчает фиксирование правильных (эталонных) реакций в технической документации и восприятие оператором результатов проверки.

Перспективным направлением в повышении обслуживаемости микропроцессорной аппаратуры и микроЭВМ является сигнатурный анализ, предполагающий использование циклических избыточных кодов для сжатия длинных двоичных кодов—реакций аппаратуры на тестовые последовательности в короткий, обычно 4-, 5-разрядный шестнадцатеричный код, который просто индицируется и сравнивается с указанным в документации для каждой контролируемой точки контрольным кодом (сигнатурой).

Математическая основа сигнатурного анализа - способ кодирования двоичных последовательностей с использованием циклических кодов. При этом любое двоичное числа описывается многочленом, содержащим фиктивную переменную х, в котором каждая двоичная цифра является коэффициентом фиктивной переменной х. Например, двоичной последовательности 1100101 (младший раз ряд слева) соответствует многочлен

х⁶+х⁵+х² + 1.

Выходной двоичной последовательности с определенного узла цифрового устройства соответствует полином G (х) степени п - 1, где п - число разрядов двоичного кода. В процессе формирования сигнатуры полином G (х) делится на порождающий полином Р(х), значение которого определяется структурой регистра сдвига с обратными связями в сигнатурном анализаторе. Для формирования четырехразрядной шестнадцатеричной сигнатуры из всего множества возможных полиномов выбирают Р(х) = = 1 + х⁶ + х⁸ + х¹¹ + х¹⁵, что соответствует обратным связям от 7, 9, 12 и 16 разрядов.

При делении G(х) на Р(х) получаем частное Q(х) и остаток R(х). Исходный полином при этом

G(х)=Р(х)Q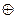(х) R(х),

где 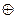— знак суммирования по модулю 2. Если в двоичном коде, соответствующем полиному G (х), возникли ошибки, то они вызывают преобразование исходного полинома G (х) в G '(х). При этом полином ошибок Ео (х} определяется как

Е₀(х) = G(х) 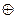G'(х) и

G'(х)=Р(х)Q'(х) 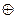R'(х) = G(х) 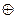Е₀ (х).

Ошибки в выходном двоичном наборе не обнаруживаются, если остатки R (х) и R '(х) совпадают, R (х) =R'(х). При этом полином Е₀(х) делится на Р(х) без остатка, и в регистре сдвига сигнатуры совпадают для правильной и ошибочной двоичных последовательностей.

Сигнатурный анализ дает высокий процент обнаружения ошибок. Для определения вероятности Р_ош обнаружения ошибки в двоичной последовательности длиной nс использованием регистра сдвига на mдвоичных триггерах воспользуемся следующим соотношением:

Р_ош=1-Н(n-m)(2^п-m-1)/(2ⁿ-1),

где функции

О при n-m <=0;

H(n-m)=

1 при n-m > 0.

При m = 16 и n = 17 лишь одна последовательность ошибок может быть упущена из 2¹⁷, при n= 18 - три, при n = = 19 — семь и т.д. Если п становится очень большим, вероятность обнаружения ошибки приближается к

Рош 1-2 ^-m = 1-2 ^-16 0,99998.

Дата добавления: 2015-09-02