Сепарация частиц пыли из криволинейного потока газа

При движении частицы пыли в криволинейном потоке газа на нее действуют две силы: аэродинамическая, обусловленная движением частицы в потоке газа со скоростью w_г, и центробежная, с которой частица стремится двигаться от центра в направлении радиуса со скоростью w_R (рис. 3.1).

Рис. 3.1. Движение частиц пыли в криволинейном потоке газа

Рассматривая движение частицы в радиальном направлении, на основании второго закона Ньютона можно написать дифференциальное уравнение следующего вида:

_, (3.1)

где М - масса частицы, кг; w_г - скорость газа, м/с; R - радиус кривизны траектории в рассматриваемой точке, м; С - аэродинамический коэффициент; F - площадь сечения частицы в направлении, нормальном к радиусу, м²; w_R - скорость движения частицы в радиальном направлении, м/с; r_г и r_ч - плотности газа и пыли (частицы), кг/м³; t - время, с.

Принимая форму частицы сферической, а движение в радиальном направлении ламинарным, в уравнение (3.1) можно подставить следующие величины:

.

После несложных преобразований будем иметь

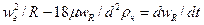. (3.2)

Принимая, что 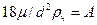; и 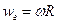, получим

. (3.3.)

В результате решения этого уравнения и ряда преобразова­ний имеем

, (3.4)

откуда

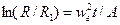. (3.5)

Следовательно,

. (3.6)

Из уравнения (3.6) можно определить, какое время t нужно для перехода частицы размером d с радиуса R₁ на радиус R или какое расстояние в радиальном направлении R — R₁ пройдет частица за время t.

Полученное выражение показывает, что сепарация улучшается с увеличением скорости газа w_г, размера частицы d и ее плотности r_ч и ухудшается с увеличением радиуса R и вязкости газа m.

Дата добавления: 2015-09-02