построение и оптимизация сетевой модели

Определение исходной длительности работ для определения исходной длительности (продолжительности) работ пользуемся формулой (1)

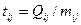
Результаты расчетов в часах следующие

t0-1=6,6	t5-10=6
t0-2=5,7	t5-13=6
t0-3=5	t6-11=4
t0-4=20	t7-11=6
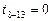
t1-6=6	t9-12=20
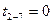
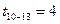
t3-7=6	t11-13=4
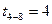
	t12-14=20
t4-9=20	t13-14=20

Построение исходной сетевой модели используя 8 правил, построим: сетевую модель по исходным данным графическим способом

Определение и анализ системных характеристик исходной сетевой модели. Определим все возможные полные пути сетевой модели, которые представим как цепочки событий от начального до конечного события:

Путь L ₁: 0 – 1 – 5 – 10 – 13 – 14;

Путь L ₂: 0 – 1 – 5 – 13 – 14;

Путь L ₃: 0 – 1 – 6 – 11 – 13 – 14;

Путь L ₄: 0 – 2 – 7 – 11 – 13 – 14;

Путь L ₅: 0 – 3 – 7 – 11 – 13 – 14;

Путь L ₆: 0 – 4 – 8 – 3 – 7 – 11 – 13 – 14;

Путь L₇: 0 – 4 – 9 – 12 – 14;

Возможных путей семь. Произведем расчеты, с помощью которых вычислим продолжительности каждого пути. Для этого воспользуемся формулой (10)

, где t_i-j – продолжительности работ данного пути (в часах).

= 6,6+4+6+4+20 =40,6 часов

=:,6 +4 +6 +20 =46,6 часов

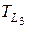= 6,6 + 6 + 4 + 4 + 20 =40.6 часов

= 5,7+0+6+4+20=35,7 часов

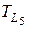=5+6+6+4+20=41 час

=20+4+0+6+6+4+20=60 часов

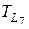= 20+20+20+20=80 часов

Выделим критический путь L_кр. Путь с наибольшей продолжительностью по времени будет являться критическим. Это путь L ₇с продолжительностью 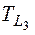= 80 часов.

Найдем среднее значение продолжительности пути . Для этого воспользуемся формулой 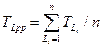, где n – количество путей. Тогда T_Lcp= 344,5/7=49,2 (часов).

Имея величину T_Lcp, рассчитаем резерв времени R_Li для каждого пути L_i. Резерв времени вычисляется по формуле R_L = T_Lcp-T_Li. Данные о продолжительности путей и резервах времени по путям приведены в таблице.

Исходные продолжительности и резервы пути.

Путь Ц	TL, (в часах)	RL (в часах)
	40,6	8,6
	46,6	2,6
	40,6	8,6
	35,7	13,5
		8,2
		-10,8
		-30,8

Отрицательное значение R_L6 и R_L7 свидетельствует о том, что этот путь критический и условный дефицит времени составляют 10,8 и 30,8 часов.

Рассчитаем характеристики событий. При определении ранних сроков наступления событий Т_pi двигаемся по сетевому графику слева направо и используем форму (2) при определении поздних сроков наступления событии Т_пi двигаемся по сетевому графику справа налево и используем формулы (3) или (3, а).

T_po=0+0=0

T_p1=0+6,6=6,6

T_p2=0+5,7=5,7

T_p3=0+5=5

T_p4=0+20=20

T_p5=0+6,6+4=10,6

T_p6=0+6,6+6=10,6

T_p7=0+5+6=11

T_p8=0+20+4=24

T_p9=0+20+20=40

T_p10=0+6,6+4+6=16,6

T_p11=0+6,6+6+4=16,6

T_p12=0+20+20+20=60

T_p13=0+6,6+4+6=16,6

T_p14=0+20+20+20+20=80

Т_п0 =80-80=0

Т_п1 =80-20-6-4=50

Т_п2 =80-20-4-6-0=50

Т_п3 =80-20-4-6-6=44

Т_п4 =80-20-20-20=20

Т_п5 =80-20-6=54

Т_п6 =80-20-4-4=52

Т_п7 =80-20-4-6=50

Т_п8 =80-20-20-20-4=16

Т_п9 =80-20-20=40

Т_п10 =80-20-4=56

Т_п11 = 80-20-4=56

Т_п12 =80-20=60

Т_п13 =80-20=60

Т_п14 =80

Ранние и поздние сроки наступления событий

Событие Lt	ТPi	Тni
	6,6
	5,7
	10,6
	12,6
	16,6
	16.6
	16,6

Вычислим максимальный запас времени, на который можно отсрочить начало или увеличить длительность каждой работ без увеличения длительности критического пути. Этот запас называется резервом времени работы и обозначается R_fJ. Для этого воспользуемся формулой (5)

Работы на критическом пути не имеют полного резерва времени, для них R_i-j = 0, тогда получаем, что

R 0-1=43,4	R 5-10=39,4
R 0-2=44,3	R 5-13=43,4
R 0-3=39	R 6-11=33,4
R 0-4=0	R 7-11=39
R 1-5=43,4	R 8-3=20
R 1-6=39,4	R 9-12=0
R 2-7=44,3	R 10-13=39,4
R 3-7=39	R 11-13=39,4
R 4-8=20	R 12-14=0
R 4-9=0	R 13-14=43,4

Оптимизация сетевой модели по критерию «минимум времени» позволяет решить задачу сокращения времени выполнения всего комплекта работ. Минимизация времени выполнения всего проекта возможна только за счет сокращения продолжительности выполнения работ, лежащих на критическом пути L_K. Для этого с ненагруженных путей мы должны снять исполнителей и равномерно распределить их по критическому пути и близким к критическому (подкритическим) путям.

Введем новые обозначения: m_l__j ↓ - исполнители, снятые с работы i-j; m_l__j ↑ -исполнители, назначенные на работу i-j; m’_l__j - новое количество исполнителей на работе i-j; t_ij - новая продолжительность работы i-j.

Количество исполнителей m_l-j ↓, которых возможно снять с работ вычислим по формуле (9). При перераспределении исполнителей необходимо соблюдать условия:

1) m'_i-j = m_i-j +m_i-j↑ - для критического пути;

2) m'_i-j = m_i-j +m_i-j ↓ - для ненагруженных путей;

3) ∑ m_i-j ↓ =∑ m_i-j↑ - общая сумма исполнителей снятых с работ ненагруженных и добавленных на работы критического пути.

m0-1 ↓=2	m5-10 ↓=1
m0-2 ↓=6	m5-13 ↓=1
m0-3 ↓=2	m6-11 ↓=3
m0-4 ↓=1	m7-11 ↓=4
m1-5 ↓=3	m8-3 ↓=0
m1-6 ↓=2	m9-12 ↓=0
m2-7 ↓=0	m10-13 ↓=4
m3-7 ↓=2	m11-13 ↓=3
m4-8 ↓=3	m12-14 ↓=1
m4-9 ↓=1	m13-14 ↓=1

Из возможных вариантов m_i-j ↓ выберем работы i-j, с которыми наиболее удобно снять исполнителей. Для этого мы проведем собственно оптимизацию данного проекта безмашинным способом, переставляя исполнителей с ненагруженных путей L_i наработы i-j критического пути L_кр.

Результаты перераспределения трудовых ресурсов (исполнителей)

i-j	Qi-j	mi-j	ti-j	mi-j ↓	mi-j ↓	mi-j↑	m'i-j	t'i-j
0-1			6,6
0-2			5,7
0-3
0-4
1-5
1-6
2-7
3-7
4-8
4-9
5-10
5-13
6-11
7-11
8-3
9-12
10-13
11-13
12-14
13-14

Определим новую продолжительность времени выполнения всех работ каждого пути после оптимизации

T_L1 =6,6 + 4 + 6 + 1 + 10 =27, 6(часов)

T_L2 = 6,6 + 4 + 3 + 10 = 23,6(часов)

T_L3 =6,6 + 3 + 4 + 4 + 10=27,6 {часов)

T_L4 =5,7 + 0 + 3 + 4 + 10 = 13,7(часов)

T_L5 = 5 + 6 + 3 + 4 + 10 = 28(часов)

T_L6 = 10 + 2 + 0 + 6 + 3 + 4 + 10 = 36(часов)

T_7i = 10 + 10 + 20 + 10 = 50(часов)

Системные характеристики исходной и оптимизированной сетевой модели

Путь Li	TLi (в часах)	T’Li (в часах)
	40,6	27,6
	46,6	23,6
	40,6	27,6
	35,7	13,7
∑	344,5	203,5
Lcp	49,2	29,1

Заключение:

Общее время выполнения комплекса работ сократилось в 2 раза.

Используемая литература:

Ключников А.В.

ОСНОВЫ МЕНЕДЖМЕНТА

Учебно-методическое пособие для студентов заочного отделения

специальности 080507.65 «Менеджмент организации»

ОПД. Ф. 01

Дата добавления: 2015-09-01