Модели VAR

Модели VAR (англ. Vector AutoRegression) возникли в ответ на критические замечания, в которых высказывались сомнения от­носительно структурного моделирования, обусловленные отсутстви­ем точных теоретических основ доказательства взаимозависимости процессов. Как следствие, при соблюдении условия идентификации уравнений могли быть получены неоднозначные спецификации.

«Теоретические ограничения, наложенные на структурные мо­дели в виде систем эконометрических уравнений, были объявлены «недостоверными» в пионерской работе К.А.Симса (Sims [1980]). В этой публикации заложены основы новой методологии структур­ного моделирования векторной авторегрессии. Основные различия между методологией Симса и структурным подходом Комиссии Коулса заключаются в следующем:

1) отсутствует априорное подразделение на эндо- и экзогенные переменные;

2) не выдвигаются нулевые условия;

3) отсутствует точная (предшествующая моделированию) эко­номическая теория, рассматриваемая в качестве теоретическо­го базиса модели»^[3].

Обобщенная модель VAR имеет вид

p

I=1

I=1

p

p

I=1

Y_1t = α₁₀ + ∑α_11i Y_1t-i + ∑ α_12i Y_2t-i + ….+ ∑α_1ri Y_{rt-I +} Ɛ_1t,

p

p

p

I=1

I=1

I=1

Y_1t = α₂₀ + ∑α_21i Y_1t-i + ∑ α_22i Y_2t-i + ….+ ∑α_2ri Y_{rt-i +} Ɛ_2t,

.

.

p

p

p

.

I=1

I=1

I=1

Y_rt = α_r0 + ∑α_r1i Y_1t-i + ∑ α_r2i Y_2t-i + ….+ ∑α_rri Y_{rt-i +} Ɛ_rt.

Модель VAR представляет собой систему из k эконометриче­ских уравнений. Одновременные зависимости (т.е. взаимозависи­мости) отсутствуют, а в роли объясняющих переменных выступа­ют только временные лаги процессов. Дополнительно предполага­ется, что порядок запаздывания одинаков для всех процессов и ра­вен р. Правая сторона модели VAR одинакова для всех уравнений.

Спецификацию модели VAR можно подвергать различным мо­дификациям. Например, в модель VAR добавляется детерминиро­ванный член, представляющий тренд и сезонность. Матричная форма такой модели имеет вид

У_t = A₁(р)У_t-1 + A₂(p)Y_t-2 +... + A_p(p)Y_t-p + ВТ + DQ + Ɛ_t,

где Y_t — вектор k процессов; T — матрица полинома относительно переменной времени t, имеющего степень r, Q- матрица двоичных сезонных переменных.

  ː ː

Y_1t 1 1 …. 1`

Y_t = Y_{2t ,} T = 1 1 …. 1`.

:: ….:

Y_rt 1 n …. n1`

Спецификацию модели VAR рекомендуется использовать для сезонных, особенно для ежемесячных данных, поскольку для мно­гих экономических категорий предположение об отсутствии одно­временных связей между ежемесячными данными является вполне оправданным. Помимо того, для оценивания модели VAR необхо­димо значительное количество наблюдений.

Рис. 11.9

Рассмотрим пример оценивания модели VAR средствами па­кета программ GRETL с применением инструкции меню Model/ Time series/ Vector Autoregression.

Модель VAK состоит из четырех уравнений дляследующих макроэкономических категорий: Y_1t- уровень безработицы; Y_2t-индекс инфляции; У _3t - объем импорта; У_4t - расходы бюджета.

Представлены данные по всей Польше с января 1993 г. по декабрь 2002 г. (n = 120)^[4].

В спецификации модели VAR в пакете программ GRETL, иллюстрируемой на рис. 11.9, необходимо отметить процес­сы, учитываемые в первом уравнении (спецификации для остальных уравнений со­ставляются автоматически).

В первую очередь опре­деляем зависимый процесс для первого уравнения (First dependent variable), далее - общий порядок запаздывания для всех процессов (lag order), детерминированные компо­ненты модели - тренд и сезон­ность (Deterministic variables), а также независимые процессы (Independent variables) для первого уравнения, которые в других уравнениях будут рассматриваться как зависимые процессы.

Окно результатов оценивания модели VAR очень велико, поскольку оно содержит оценки по четырем уравнениям, их ме­ры соответствия эмпирическим данным и тесты значимости, а также результаты оценивания функции импульсных откликов для каждого процесса (impuls responses) и декомпозицию дис­персии по методу Холеского (Cholesky) для каждого процесса. Оцениваемые уравнения содержат большое количество парамет­ров: четыре временных лага процессов 12-го порядка (48 пара­метров), линейный тренд (2 параметра), ежемесячные сезонные переменные (11 параметров). Количество степеней свободы равно s = 108 - (48 + 2 + 11) = 108 - 61 =47. Фрагменты результатов только для первого уравнения представлены на рис. 11.10.

Оценки параметров и их погрешности свидетельствуют о при­сутствии в уравнении множества несущественных переменных, од­нако глобальные оценки указывают на высокую степень соответст­вия модели эмпирическим данным (R² = 0,9987) и на отсутствие

Рис. 11.10

автокорреляции в процессе остатков (DW = 1,979, р₁ = 0,0049). Для каждого уравнения также представляются результаты провер­ки принятого порядка временного лага р = 12.

11.2.1. Проверка значимости временного лага порядка р

В модели VAR необходимо проверять принятый порядок вре­менного лага р, который остается одинаковым для всех перемен­ных. Эта процедура выполняется следующим образом.

По спецификации первого уравнения модели VAR оценивают­ся вспомогательные уравнения, для которых делаются следующие предположения:

/

• все параметры при переменной с запаздыванием для уровня безработицы равны пулю:

Н₀: α_11i = 0, H ₁ : α_11i = 0, для i = 1,2.................................. 12;

• проверочная статистика имеет вид

F = (RSS_r - RSS_var)/p

RSS_VAR/S

где RSS_r - сумма квадратов остатков уравнения с ограничениями (α_11i = 0); RSS_var - сумма квадратов остатков уравнения VAR (α_11i = 0); р - порядок временного лага; 5 - количество степеней свободы в уравнении VAR.

Если критическое значение для распределения F(p, s) > F, то тест свидетельствует о значимости временного лага, введенного в уравнение VAR.

Если в в каждом уравнении для исследуемого комплекса про­цессов содержится такая переменная, которая оказывается несу­щественной, то ее можно признать экзогенной переменной для этого комплекса процессов.

10000-

-5000

Значимость максимального запаздывания в модели VAR про­веряется при помощи F-теста для следующих гипотез:

Н₀: α_1jp = 0, H ₁ : α_1jp = 0, для j = 1,2..................................., R,

где р - порядок максимального запаздывания в модели VAR.

В рассматриваемом примере принятый порядок запаздывания р = 12 достаточен, поскольку результат выполнения F-теста свиде­тельствует о его существенности, а в процессах остатков всех урав­нений отсутствует существенная автокорреляция.

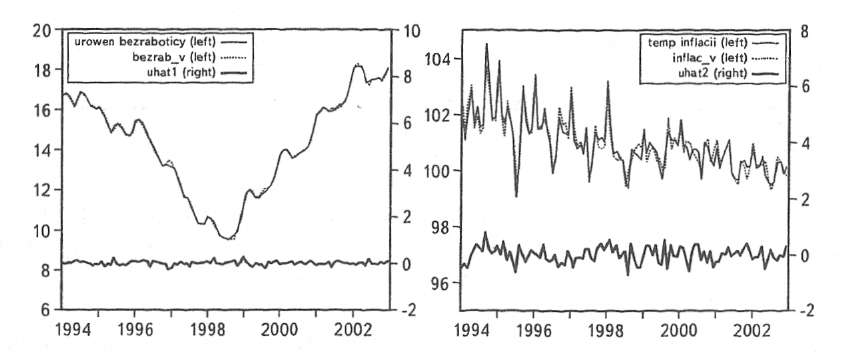
На рис. 11.11 представлены графики, иллюстрирующие сте­пень соответствия уравнений эмпирическим данным. Эти графики построены при выполнении функции Data/Graph specified vars/Time series plot... для эмпирических и теоретических про­цессов, а также для остатков, полученных но модели VAR.

11.2.2. Функция импульсных откликов в модели VAR

В окне модели VAR представляются результаты оценивания функции импульсных откликов (impuls responses)^[5] для каждой пе­ременной по отношению ко всем факторам. Величина импульса находится на уровне одной стандартной погрешности остатков. На рис. 11.12 приведены результаты, демонстрирующие измене­ния для уровня безработицы.

Каждую функцию импульсных откликов можно представить в текстовом окне (см. рис. 11.12) и в виде графика (табл. 11.1). Графики для выбранных комбинаций переменных можно полу­чить в окне модели VAR при помощи функции Graphs/ response of d_var/to d_var так, как это демонстрируется на рис. 11.13.

Комбинации графиков импульсных откликов представлены в табл. 11.1.

Результаты декомпозиции дисперсии для каждой переменной модели, полученные с применением метода Холеского^[6], представ­лены на рис. 11.14.

Пакет программ GRETL также позволяет декомпозировать дисперсию с применением метода QR. Требуемый метод необходимо указать наряду с другими общими параметрами пакета программ (рис.1.12)

Рис. 11.12

Рис. 11.13

Отметим, что пакет программ GRETL позволяет достаточно просто оценить модель VAR, однако необходимость ее представле­ния в сокращенной форме без возможности наложения ограничений

Таблица 11.1

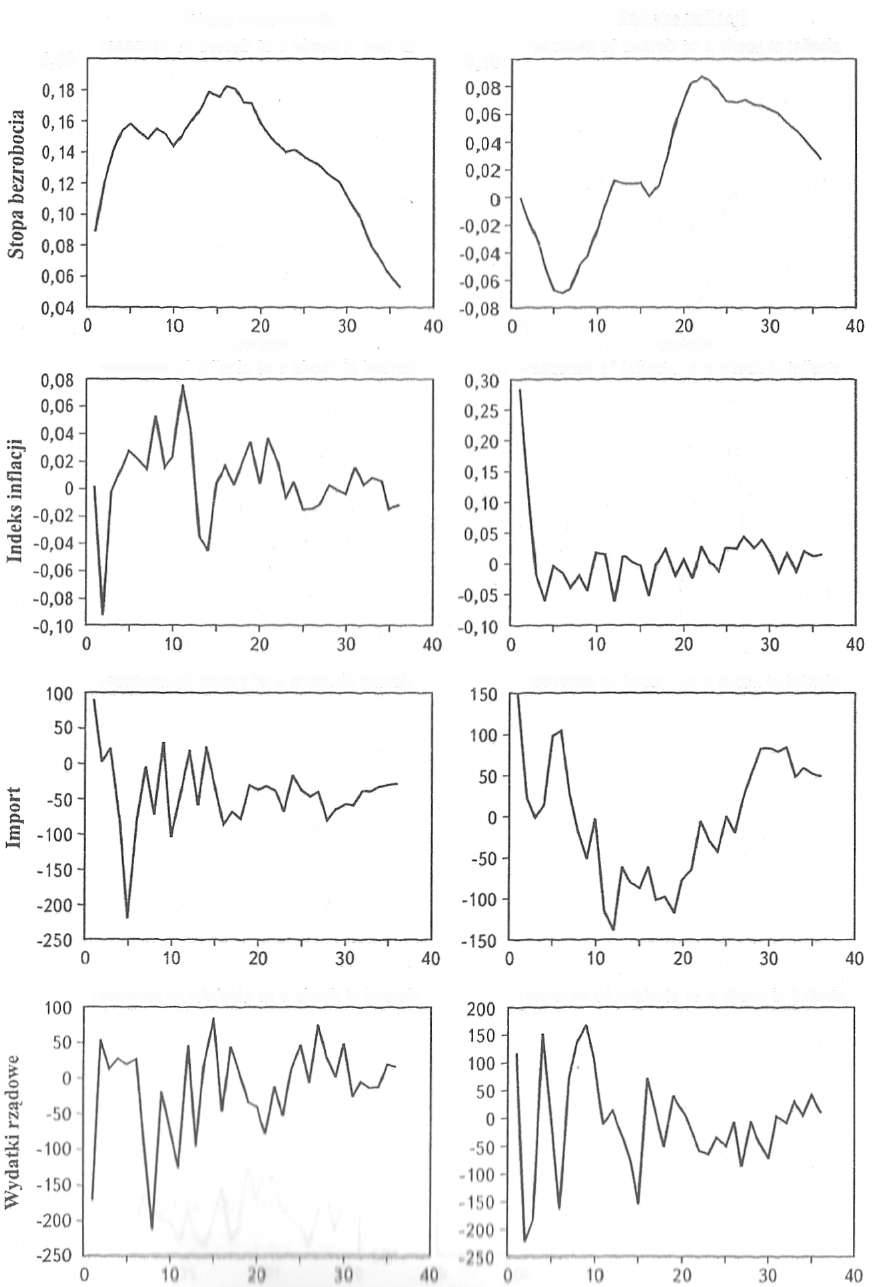Комбинации импульсных откликов

Окончание табл. 11.1

Источник: собственная разработка

Рис. 11.14

сужает область возможных приложений. Для квартальных и еже­месячных данных может применяться «близкая к теоретической» модель в сокращенной форме.

Пакет программ GRETL позволяет выполнять множество дру­гих функций, которые не упоминались в этой книге ввиду специ­фичности их тематики, не всегда изучаемой в курсе эконометрики. К ним относятся: проблематика анализа коинтеграции, панельные модели, метод главных компонентов, а также вопросы работы с языком команд, очень удобным для проведения имитационного анализа.

По мнению многих пользователей, бесплатный пакет программ GRETL очень удобен в работе, а представляемые результаты на­глядны и полны. Хочется надеяться, что настоящая публикация облегчи! его настоящим и будущим пользователям изучение эко­нометрики, а также повысит результативность проводимого чис­ленного анализа экономических процессов.

^[1] С более детальной классификацией моделей и переменных можно познакомиться но многих учебниках но эконометрике.

^[2] Файл przemysl_chemiczny_rus.gdt доступен на сайте www.kufel.torun.pl.

^[3] См. Cbaremza, Deadman [1997], с. 152. ^{[3] 3} См. Charemza, Deadman [1997], с. 152.

^[4] Файл macro_1993_2002_rus.gdt доступен на сайте www.kufel.torun.pl.

^[5] См. Greene [2003] с. 593-595.

^[6] См. Hendry [1997], с. 631, Enders [1995] с. 305-354.

Дата добавления: 2015-09-02