Компенсация реактивной мощности нагрузки

Рассмотрим схему замещения ЛЭП без емкостных элементов, рис. 5.15. Это допустимо, если нас интересует лишь величина потери напряжения в линии. На рис. 2.5 строилась векторная диаграмма линии при вариации реактивной мощности и заданном напряжении в конце линии. Анализ построенной векторной диаграммы показал, что изменение реактивной мощности в конце линии оказывает существенное влияние на величину напряжений в линии.

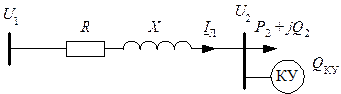Рис. 5.15. Схема замещения линии без емкостных элементов

Оценим изменение величины потери напряжения в линии при установке на шинах нагрузки КУ. Построим для этого векторные диаграммы токов и напряжений в линии для двух случаев: первую без компенсации реактивной мощности и вторую – с компенсацией половины реактивной мощности нагрузки Q _КУ = 0,5 Q _Н, рис. 5.16.

Рис. 5.16. Векторная диаграмма токов и напряжений линии при компенсации

реактивной мощности нагрузки

Ток в линии I _л вычисляется через мощность S ₂ = P ₂ + jQ ₂:

Для удобства построения векторных диаграмм совместим с действительной осью вектор напряжения U ₂. Построим треугольник падения напряжения на активном сопротивлении для первого случая – вектор падения напряжения на активном сопротивлении D U _R – параллельно току линии I _л, а вектор падения напряжения на реактивном сопротивлении D U _X – с опережением вектора тока I _л на 90°.

Сумма векторов U ₂ и D U = D U _R + D U _X есть вектор напряжения в начале линии U ₁^(a). Конец этого вектора отмечен на диаграмме точкой A.

Далее построим треугольник падения напряжения и напряжение в начале линии для тока линии I _л1, который имеет ту же самую вещественную составляющую I ¢ _л и вдвое меньшую мнимую составляющую I ² _л1:

Конец вектора U ₂^{( b )} отмечен точкой B.

Отложим величины обоих векторов напряжения в начале линии по вещественной оси: отрезки, равные U ₁^{( a )}.и U ₁^{( b )}, и сопоставим между собой потери напряжения для обоих случаев.

Отрезок O′A′ является потерей напряжения в первоначальном режиме (без компенсации Q _Н), а отрезок O′B′ – потерей напряжения во втором случае (при компенсации Q _Н). Очевидно, что длина отрезка O′A′ больше длины отрезка O′B′, т.е. потеря напряжения во втором случае существенно меньше, чем в первом.

Те же самые выводы можно сделать и для режима, когда неизменным поддерживается напряжение в начале линии, а напряжение U ₂ изменяется при компенсации реактивной мощности нагрузки. Модуль U ₂ можно получить из соотношения:

Из последнего выражения (5.16) также видно, что с уменьшением реактивной составляющей тока I ″_л увеличиваются оба слагаемых в подкоренном выражении, а следовательно напряжение U ₂ возрастает.

Дата добавления: 2015-09-01