Краткие сведения из теории

С точки зрения восприятия давления плоские днища менее рациональны, чем все остальные.

В аппаратах, работающих под давлением, они применяются лишь при малых диаметрах. В аппаратах, работающих под атмосферным давлением и под наливом, устанавливаемых на основании, они применяются и при больших диаметрах.

а б в г

Рис. 1. Конструкции днищ:

а – с односторонним угловым швом; б, в – с двусторонним угловым швом;

г – с односторонним стыковым швом в замок

В основу расчета плоских днищ положена теория изгиба круглых, симметрично нагруженных пластин.

Рассмотрим (рис. 2) пластину постоянной толщины s, нагруженную равномерно распределенной нагрузкой – давлением р.

Под действием давления пластина меняет свою кривизну одновременно в двух направлениях: радиальном и кольцевом, в результате чего образуется слабо изогнутая поверхность двоякой кривизны. Если в такой пластине двумя радиальными и двумя кольцевыми сечениями выделить элемент (рис. 3), на его грани будут действовать радиальный 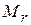и кольцевой изгибающие моменты и поперечные силы 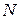. Им соответствуют радиальные и кольцевые нормальные напряжения и касательные напряжения . При расчете прочности пластин учитывают лишь радиальные и кольцевые моменты и напряжения, величина касательных напряжений обычно невелика.

Рис. 2. Схема нагружения круглой пластины давлением

Рис. 3. Схема нагружения элемента пластины

Изгибающие моменты 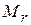и определяются путем совместного решения уравнений равновесия сил и моментов, действующих на выделенный элемент с использованием закона Гука и граничных условий. Результаты решения имеют следующий вид:

– для случая защемленного контура пластины (рис. 4, а)

, (1)

; (2)

– для случая свободного опирания контура пластины (рис. 4, б)

, (3)

, (4)

где – коэффициент Пуассона.

а б

Рис. 4. Схемы и эпюры плоских днищ:

а – защемленный контур; б – свободное опирание контура

Наибольшие напряжения, возникающие на различных поверхностях пластины, связаны с изгиба­ющими моментами соотношениями:

; . (5)

При расчете напряжений в пластинах (рис. 4) знак плюс в формулах (5) относится к наружной (нижней) поверхности, а знак минус – к внутренней (верхней) поверхности.

В основу расчета пластин (и плоских днищ), изготовленных из пластичных материалов, положена теория наибольших касательных напряжений (третья теория прочности), согласно которой эквивалентные напряжения

, (6)

где , – наибольшее и наименьшее главные напряжения.

В пластине, находящейся в плоском напряженном состоянии, .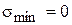

Тогда

. (7)

Для случая защемленного контура наибольшее растягивающее напряжение возникает на внутренней поверхности пластины вблизи контура:

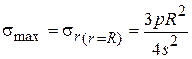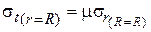; . (8)

Для случая свободного опирания контура наибольшее растягивающее напряжение возникает на наружной поверхности в центре пластины:

. (9)

Таким образом, учитывая, что R = D /2, а = 0,3, для обоих случаев справедливо следующее выражение:

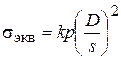, (10)

где k – коэффициент.

Из (10) и условия прочности 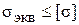расчетная толщина пластины может быть определена как

, (11)

где k – коэффициент, учитывающий способ закрепления края пластины: для защемленного контура – из формулы (8) ; для свободного опирания – из формулы (9) .

Согласно ГОСТ 14249-89, расчетную толщину плоского днища определяют по формуле

, (12)

где k – коэффициент конструкции днища; k _о – коэффициент ослабления днища отверстиями; D _р – расчетный диаметр (внутренний диаметр обечайки); 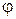– коэффициент прочности сварного шва.

Для днищ (крышек), имеющих одно отверстие диаметром d,

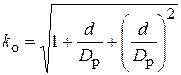. (13)

В случае, когда несколько отверстий диаметром ,

. (14)

Коэффициент k _о определяют для наиболее ослабленного диаметрального сечения днища.

Для днища экспериментального сосуда лабораторной установки

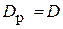_, k _о 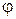= 1, = 1.

Дата добавления: 2015-09-02