Тенденции развития 7 страница

– накопители на оптических дисках;

– прочие запоминающие устройства.

Сетевые запоминающие устройства:

– накопители на жестких дисках;

– накопители на магнитной ленте;

– накопители на оптических дисках:

– прочие сетевые запоминающие устройства.

Локальные печатающие устройства:

– принтер.

Сетевые печатающие устройства печати:

– сервер печати;

– сетевой принтер;

– принтер;

– другие сетевые устройства печати.

Сетевые распределительные компоненты:

– мост;

– коммутатор;

– маршрутизатор;

– повторитель;

– модем;

– мультиплексор;

– узел коммутации ATM;

– узел коммутации Х.25;

– оконечный сетевой элемент;

– спутниковая станция связи;

– станция радиосвязи;

– прочие сетевые распределительные компоненты.

Сетевые шлюзы:

– шлюз трансляции сообщений;

– шлюз трансляции адресов;

– шлюз безопасности;

– управляющий шлюз;

– шлюз преобразования протоколов;

– прочие шлюзы.

Управление сетью и управляющие серверы:

– системы, обеспечивающие протоколирование сообщений и управление сообщениями;

– сетевые серверы аутентификации;

– сетевой центр управления;

– другие средства сетевого управления и управляющие серверы.

Сетевые интерфейсы:

– постоянное соединение:

- синхронное;

- асинхронное.

– коммутируемое соединение:

- PSTN;

- ISDN;

- радиосоединение;

– прочие типы соединений.

Сетевые сервисы:

– объединение локальных сетей;

– канал с невысокой пропускной способностью;

– канал с пропускной способностью, соответствующий предъявляемым требованиям;

– маршрутизация сообщений;

– сетевое хранилище;

Сервисы общего назначения:

– Internet;

– другие сети общего назначения;

– телефония;

– прочие сетевые сервисы.

Сервисы конечного пользователя:

– электронная почта;

– прикладной обмен сообщениями;

– обмен электронными документами;

– передача файлов;

– сеансовая обработка;

– пакетная обработка;

– голос;

– видео;

– прочие сервисы конечного пользователя.

Коммуникационные протоколы:

– Х.25;

– SDLS/HDLS;

– IP;

– CLNP (Connectionless Network Protocol);

– ATM;

– Frame Relay;

– TDM;

– протоколы спутникового обмена информацией;

– Ethernet;

– Token Ring;

– прочие протоколы.

Носители данных (Media):

– неэлектронные носители:

- устройства ввода;

- устройства вывода;

- важные записи;

- прочие виды носителей;

– электронные носители:

- магнитные ленты;

- диски;

- прочие виды носителей.

Классы угроз

– использование чужого идентификатора сотрудниками организации (маскарад);

– использование чужого идентификатора поставщиком услуг (маскарад);

– использование чужого идентификатора посторонними (маскарад);

– несанкционированный доступ к приложению;

– внедрение вредоносного программного обеспечения;

– несанкционированное использование системных ресурсов;

– использование телекоммуникаций для несанкционированного доступа сотрудниками организации;

– использование телекоммуникаций для несанкционированного доступа поставщиком услуг;

– использование телекоммуникаций для несанкционированного доступа посторонними;

– ошибки при маршрутизации;

– неисправность сервера;

– неисправность сетевого сервера;

– неисправность запоминающих устройств;

– неисправность печатающих устройств;

– неисправность сетевых распределяющих компонент;

– неисправность сетевых шлюзов;

– неисправность средств сетевого управления или управляющих серверов;

– неисправность сетевых интерфейсов;

– неисправность сетевых сервисов;

– неисправность электропитания;

– неисправность кондиционеров;

– сбои системного и сетевого ПО;

– сбои прикладного ПО;

– ошибки пользователей;

– пожар;

– затопление;

– природные катаклизмы;

– нехватка персонала;

– кражи со стороны сотрудников;

– кражи со стороны посторонних;

– преднамеренные несанкционированные действия сотрудников;

– преднамеренные несанкционированные действия посторонних;

– терроризм.

Классы контрмер

– идентификация и аутентификация;

– логическое управление доступом;

– протоколирование;

– аудит;

– безопасность многократного использования объектов;

– тестирование систем;

– контроль целостности ПО;

– управление вводом/выводом;

– управление безопасностью в сети;

– обеспечение безотказности;

– обеспечение конфиденциальности вне соединения;

– управление доступом в сети;

– физическая безопасность сети;

– защита сообщений;

– обеспечение целостности данных вне соединения;

– сохранение правильной последовательности сообщений;

– пополнение трафика;

– контроль операций в системе;

– контроль действий системного администратора;

– контроль действий прикладных программистов;

– контроль операций по поддержке прикладного ПО;

– контроль операций по обслуживанию СВТ;

– контроль пользователей;

– контроль ввода/вывода приложений;

– финансовая отчетность;

– контроль выходных документов;

– контроль носителей данных;

– контроль транспортировки физических носителей данных;

– резервное копирование и восстановление ресурсов сервера;

– резервирование и восстановление сетевых интерфейсов;

– резервирование и восстановление сетевых сервисов;

– восстановление помещений;

– резервирование и восстановление носителей данных;

– планирование восстановления;

– резервное копирование данных;

– планирование потребностей в ресурсах;

– защита от сбоев СВТ;

– обеспечение физической безопасности помещений;

– оптимизация расположения СВТ в помещениях;

– организация зон безопасности;

– защита от краж;

– физическая защита СВТ;

– контрмеры против террористов и экстремистов;

– защита средств контроля доставки;

– обнаружение бомб и взрывчатых веществ;

– защита от минирования со стороны сотрудников и посторонних лиц;

– защита от пожара;

– защита от затоплений;

– защита от природных катаклизмов;

– защита источников электропитания;

– защита поддерживающей инфраструктуры;

– защита персонала;

– обучение персонала;

– политика безопасности;

– инфраструктура безопасности;

– оповещение об инцидентах;

– проверка жалоб.

Приложение 6
Оценка рисков экспертными методами

Оценка субъективной вероятности

Как правило, на практике субъективную вероятность приходится привлекать в следующих случаях:

– когда объективная вероятность некачественная;

– если предполагается, что полученные закономерности и объективная вероятность не будут наблюдаться в будущем;

– когда нет объективных данных о наблюдениях в прошлом.

В таких ситуациях субъективную вероятность можно рассматривать как меру уверенности эксперта в возможности наступления события. Она может быть представлена по-разному: вероятностным распределением на множестве событий, бинарным отношением на множестве событий, не полностью заданным вероятностным распределением или бинарным отношением и другими способами.

Покажем, как определить субъективную вероятность. Разделим процесс на три этапа:

– подготовительный этап;

– получение оценок;

– анализ оценок.

Первый этап позволяет выделить объект исследования - некоторое множество событий. Далее проводится предварительный анализ свойств этого множества (устанавливается зависимость или независимость событий, дискретность или непрерывность случайной величины, порождающей данное множество событий). На основе такого анализа выбирается один из подходящих методов определения субъективной вероятности. На этом же этапе проводится подготовка эксперта или группы экспертов, ознакомление его с методом и проверка понимания поставленной задачи экспертами.

Второй этап состоит в применении метода, выбранного на первом этапе. Результатом этого этапа является набор чисел, который отражает субъективный взгляд эксперта или группы экспертов на вероятность того или иного события. Здесь далеко не всегда удается установить окончательное распределение, поскольку результаты могут быть противоречивыми.

Третий этап заключается в исследовании и обобщении результатов опроса. Если вероятности, представленные экспертами, не согласуются с аксиомами вероятности, то это доводится до сведения экспертов и ответ уточняются так, чтобы они соответствовали аксиомам. Для некоторых методов определения субъективной вероятности третий этап исключается, поскольку сам метод состоит в выборе распределения, подчиняющегося аксиомам вероятности, которое в том или другом смысле наиболее близко к оценкам экспертов. Примеры таких методов -метод главного значения для конечного множества независимых событий и минимаксный метод для зависимых событий. Особую важность третий этап приобретает при агрегировании оценок, полученных от группы экспертов. Например, в методе Делфи, после анализа вероятностей, представленных отдельными экспертами, предполагается повторение второго этапа, то есть повторный опрос. Далее вновь следует третий этап, и в случае необходимости процедура выполняется еще раз.

Классификация методов получения субъективной вероятности

Методы определения субъективной вероятности можно классифицировать в зависимости от формы поставленных перед экспертами вопросов или от характеристик событий и случайных величин, а также от числа привлекаемых экспертов. В задачах оценки рисков в условиях неопределенности требуется оценивать вероятность (возможность) состояний внешней среды (неопределенных факторов). Поскольку внешняя среда может принимать лишь одно значение из заданного множества, то при оценке субъективных вероятностей обычно применяют методы, предназначенные для множеств несовместных событий. Среди методов, служащих для оценки вероятностей в случае конечных множеств несовместных событий, наибольшее практическое значение имеют три: метод прямого приписывания вероятностей, метод отношений и метод собственного значения, а в случае бесконечных множеств несовместных событий - метод изменяющегося интервала и метод фиксированного интервала.

Для практической реализации указанных методов необходима их детальная доработка и адаптация к характеру решаемых задач. Также понадобится разработать и реализовать конкретные алгоритмы проведения опроса экспертов по этим методам. В качестве дополнения к таким алгоритмам нужны процедуры графического представления данных, подготовленных экспертом. Это позволит эксперту вносить необходимые корректировки в свои прежние оценки исходя из общей картины. А для обработки вероятностей, представленных несколькими экспертами, следует создавать процедуры агрегирования вероятностей. В их основу может быть положен метод взвешенной суммы. Для лучшей согласованности оценок экспертов обычно разрабатывают итеративную процедуру проведения экспертизы, основанную на методе Делфи.

Условно методы нахождения субъективной вероятности можно разделить на следующие три группы.

Первая, самая многочисленная группа, - это прямые методы, состоящие в том, что эксперт отвечает на вопрос о вероятности события. К ним относятся метод изменяющихся интервалов, метод фиксированных интервалов, метод отношений, графический метод, метод собственного значения, методы оценки параметров распределения и др. Независимо от конкретного метода данной группы эксперт должен оценивать непосредственно вероятность событий.

Вторую группу образуют методы, в которых вероятность событий выводится из решений экспертов в гипотетической ситуации. Примером является метод лотерей, а также метод равноценной корзины. Формально говоря, применение методов второй группы требует от эксперта сравнения не вероятностей как таковых, а полезности альтернатив, при которых исход зависит от реализации случайной величины. Многие эксперты отмечают возрастающую сложность вопросов и более существенные ошибки при применении этих методов по сравнению с методами первой группы.

Третья группа - это гибридные методы, требующие от экспертов ответов на вопросы как о вероятности, так и о полезности. К гибридным методам относятся некоторые разновидности метода лотерей.

Методы получения субъективной вероятности

Постановка задачи заключается в том, что путем опроса экспертов следует построить вероятностное распределение на конечном множестве несовместимых (взаимоисключающих) событий.

Прямая оценка вероятностей событий

В этом методе эксперту или группе экспертов предъявляется список всех событий. Эксперт должен указать последовательно вероятность всех событий. Возможны различные модификации метода. В одной из модификаций предлагается сначала выбрать наиболее вероятное событие из предложенного списка, а затем оценить его вероятность. После этого событие из списка удаляется, а к оставшемуся списку применяется уже описанная процедура. Сумма всех полученных вероятностей должна равняться единице.

Метод отношений

Эксперту сначала предлагается выбрать наиболее вероятное событие. Этому событию приписывается неизвестная вероятность Р1. Затем эксперт должен оценить отношения вероятностей всех остальных событий к вероятности Р1 выделенного события (коэффициенты С2,..., CN ). С учетом того, что сумма вероятностей равна 1, составляется уравнение:

Pl(l + C2 + СЗ +... +СN) = 1.

Решив это уравнение и найдя величину P1, можно вычислить искомые вероятности.

Метод собственного значения

Метод основан на том, что неизвестный вектор вероятностей (P1,..., Рп) является собственным вектором некоторой специально построенной матрицы, отвечающим ее наибольшему собственному значению. Сначала эксперту задается вопрос, какое из двух событий более вероятно. Предположим, что более вероятно событие S1. Затем эксперта спрашивают, во сколько раз событие S1 вероятнее, чем S2. Полученное от эксперта отношение записывается на соответствующее место в матрице.

Метод равноценной корзины

Этот метод позволяет получить вероятность исходя из экспертного сравнения полезности альтернатив. Предположим, надо вычислить вероятность некоторого события S1. Определим какие-либо два выигрыша, в частности денежных, которые существенно различны, например: первый выигрыш - 1 млн. руб., а второй -0 руб., и предложим эксперту на выбор участие в одной из двух лотерей. Первая лотерея состоит в том, что выигрыш в 1 млн. руб. эксперт получает, если состоится событие S1, а выигрыш в 0 руб. - если событие не происходит. Для организации второй лотереи представим себе гипотетическую корзину, заполненную белыми и черными шарами, первоначально в равном количестве, скажем, по 50 шаров каждого цвета. Если вынутый шар белый, то участнику достается 1 млн. руб., если черный - 0 руб. Эксперта просят отдать предпочтение одной из двух лотерей. Если с точки зрения эксперта лотереи равноценны, делается вывод о том, что вероятность события S1 равна 0,5. Если эксперт выбирает первую лотерею, то из корзины вынимается часть черных шаров и заменяется тем же количеством белых. Если предпочтение отдается второй лотерее, то часть белых шаров заменяется черными. В обоих случаях эксперту вновь предлагается поучаствовать в одной из двух лотерей. Изменяя соотношение шаров в гипотетической корзине, добиваются равноценности двух лотерей. Тогда искомая вероятность события S1 равна доле белых шаров в общем их количестве.

Методы оценок непрерывных распределений

Данные методы можно использовать, например, чтобы найти функцию распределения (или плотность распределения) субъективных вероятностей некоторой непрерывной случайной величины. Чаще всего для решения такой задачи применяются два метода, основанных на опросе экспертов: метод изменяющегося интервала и метод фиксированного интервала.

Метод изменяющегося интервала

Существует несколько модификаций этого метода. Но для них общим является требование к эксперту указать на множестве значений случайной величины такой интервал, чтобы вероятность того, что случайная величина принимает значение в указанном интервале, была равна заданной величине. Например, опрос эксперта может строиться по следующей схеме. Сначала эксперта просят указать такое значение S1 случайной величины, при котором оказываются равными две вероятности: того, что случайная величина примет значение меньше S1, и того, что она примет значение больше S1. Получив от эксперта значение S1, переходят ко второму этапу. На этом этапе у эксперта спрашивают, при каком значении S2 случайной величины область значений больше S1поделится на две равновероятные части. Точно так же поступают с областью значений меньше S1и находят значение S3. Вслед за вторым этапом проводится третий этап, состоящий в нахождении медиан каждого из образовавшихся участков. Этот процесс не следует продолжать слишком долго, поскольку при малых величинах интервалов возрастает вероятность ошибки эксперта. При использовании данного метода обычно бывает полезно вернуться к предыдущим оценкам и проанализировать их непротиворечивость. В случае обнаружения противоречий эксперт должен изменить одну из своих прежних оценок.

В некоторых вариантах метода изменяющегося интервала перед экспертом может быть поставлена задача указать две точки на предложенном множестве значений случайной величины, которые разбивают это множество на три равновероятные части. В других вариантах эксперта могут, например, спросить, при каком значении случайной величины S1вероятность того, что случайная величина примет меньшее значение, чем S1, равна 0,1. Оценки, полученные таким способом, меньше зависят друг от друга, то есть не происходит накопления ошибки. В этом и заключается их преимущество. Существуют модификации метода, основанные на предположении, что для эксперта проще указать точку, делящую область на две равновероятные части, чем точку, отделяющую область, соответствующую вероятности 0,1, от остального множества. Таким образом, в случае применения метода изменяющегося интервала приходится выбирать между простотой сравнения и независимостью получаемых оценок.

Метод фиксированного интервала

В соответствии с этим методом множество значений случайной величины разбивается на интервалы и эксперта просят оценить вероятность того, что случайная величина примет значение из данного интервала. Обычно интервалы, за исключением крайних слева и справа, выбираются равной длины. Число интервалов определяется с учетом необходимой точности и требуемого вида распределения. После того как эксперт сообщил вероятность всех интервалов, обычно проводят проверку полученного распределения. Например, если двум различным интервалам приписана одинаковая вероятность, можно спросить у эксперта, действительно ли они равновероятны. Относительно других интервалов можно уточнить, действительно ли один из них во столько-то раз более вероятен, чем другой, как это следует из приписанных этим интервалам вероятностей. В результате такого просмотра эксперт может несколько подправить вероятности. Иногда метод фиксированного интервала применяется совместно с методом изменяющегося интервала. Так, можно сначала предложить эксперту определить медиану, то есть такое значение случайной величины, которое разбивает все множество значений на два равновероятных множества, а затем от найденной медианы отложить в обе стороны равные фиксированные интервалы.

Графический метод

Метод дает надежные результаты в том случае, когда эксперт хорошо подготовлен к восприятию графической информации о вероятности. Состоит он в том, что эксперт должен изобразить в графической форме (в виде графика функции распределения или плотности вероятности, в форме диаграммы или графа) свое представление о вероятности событий или о случайной величине. Зачастую общий вид графика известен, а от эксперта требуется лишь подобрать параметры распределения. Графический метод особенно полезен в качестве вспомогательного при анализе вероятностей, найденных каким-либо другим способом. Например, функция распределения может быть определена методом фиксированного интервала, а затем ее график, а также график функции плотности распределения представляют эксперту для окончательной доработки.

Некоторые рекомендации

Известно, что субъективная вероятность, получаемая экспертным путем, существенно зависит от используемого метода. В частности, эксперт нередко склонен преувеличивать вероятность наименее вероятного события, а также недооценивать вероятность наиболее вероятного или преувеличивать дисперсию оцениваемой случайной величины. Рассмотрим несколько рекомендаций, выполнение которых позволит корректно проводить опрос эксперта с помощью различных методов:

– необходимо обучить эксперта процедуре проведения экспертизы. Особенно это касается экспертов, имеющих слабую подготовку по теории вероятностей;

– надо отдавать себе отчет в том, что сама процедура опроса эксперта является лишь одним звеном во всем процессе определения вероятностей. Предшествующие шаги по вычленению событий и выбору подходящего метода столь же важны. Нельзя пренебрегать также и последующим анализом полученных вероятностей с целью возможной их корректировки;

– старайтесь применять объективную информацию о вероятностях событий, например данные о том, как такие события происходили в прошлом. Эта информация должна быть доведена до эксперта. Не забывайте также обрабатывать алгебраическим путем предыдущие оценки эксперта, чтобы сопоставить их с его новыми оценками;

– для проверки надежности представленных данных рекомендуется обращаться к каким-либо другим методам нахождения субъективной вероятности или даже к модификации методов. Определенные различными методами вероятности необходимо показать эксперту для уточнения его оценок;

– при выборе конкретного метода нужно учитывать опыт работы эксперта с числовыми показателями. И если такой опыт недостаточен, то метод фиксированного интервала непригоден, так как предполагает числовые оценки. Более подходящим в этом случае будет метод изменяющегося интервала, поскольку в его рамках от эксперта требуется лишь утверждение о равновероятности двух интервалов. В любом случае употребление знакомых эксперту понятий, фраз, вопросов и шкал облегчает возможности численного представления вероятности;

– всегда, когда это возможно, старайтесь получать субъективную вероятность от нескольких экспертов, а затем некоторым образом агрегировать ее в одну;

– сложные методы, требующие больших усилий от эксперта, например метод лотерей, лучше не применять, за исключением случаев, когда имеются серьезные аргументы в пользу выбора этих методов.

Выполнение этих рекомендаций позволяет существенно улучшить оценки вероятности.

Агрегирование субъективных вероятностей

Проблема агрегирования возникает в том случае, когда m экспертов оценивают вероятности на одном множестве событий. Существуют различные подходы к решению этой задачи:

– индивидуальные оценки рассматриваются как случайные величины на одном и том же вероятностном пространстве. Групповая вероятность представляет собой условную вероятность события S1 в предположении, что индивидуальные оценки равны Р1 ,..., Рт;

– в методе взвешенной суммы групповая вероятность находится по формуле: ,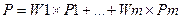

где Wi - это веса (коэффициенты компетентности), приписанные эксперту i. Если оценки Pi являются несмещенными, то веса можно принимать так, чтобы минимизировать дисперсию величины Р. На практике веса следует выбирать на основе анализа оценок экспертов, полученных во время предыдущих экспертиз;

– в подходе, основанном на методе Делфи, субъективные вероятности, представленные экспертами, доводятся до сведения всех экспертов, после чего эксперты вновь сообщают свои вероятности. Таким образом выполняется итеративная процедура, которая позволяет каждому отдельному эксперту скорректировать свои оценки после ознакомления с оценками остальных.

Методы теории полезности

При решении задач выбора в условиях неопределенности и, в частности, задачи оценки рисков наиболее обоснован подход, базирующийся на теории полезности. В настоящее время теория полезности достигла весьма высокого уровня развития. Вопросы практического применения данной теории хорошо освещены в литературе: введены понятия и исследованы свойства, позволяющие разбить процесс построения функции (одномерной) полезности на этапы и сделать его максимально эффективным; разработаны методы построения, опирающиеся на эти понятия и свойства. Теоретические результаты и методы практического построения функции одномерной полезности достаточно апробированы при решении различных задач принятия решений, и их целесообразно применять в разных методиках оценивания рисков.

Постановка задачи выбора в условиях риска

Рассмотрим следующую постановку задачи.

Задано множество 5 возможных детерминированных исходов (последствий). В роли этого множества чаще всего выступает множество значений скалярного или векторного критерия, при помощи которого оценивается эффективность (качество и т.п.) вариантов решений (стратегий, планов, альтернатив и т.д.). Достигаемый исход зависит не только от реализуемого варианта решения, но и от того, какое значение примут неопределенные (случайные) факторы, распределения вероятностей которых известны. Поэтому удобно полагать, что каждому варианту решения из допустимого множества ставится в соответствие некоторая вероятностная мера, заданная на множестве 5 (например, распределение вероятностей или плотность вероятности). Принимающий решение должен выбрать наилучший вариант из множества 5 или, что эквивалентно, сделать выбор на множестве соответствующих элементам этого подмножества вероятностных мер.

Известны два основных подхода к принятию решений при риске:

– базирующийся на применении так называемых объективных критериев выбора (привлечение различных моделей стохастического программирования, применение критериев типа математического ожидания, дисперсии и т.д.);

– основанный на получении и использовании информации субъективного характера - сведений о структуре предпочтений (лицо, принимающее решение (ЛПР)), в том числе о его отношении к риску.

Как показывают многочисленные исследования, методы, реализующие первый подход, менее надежны, поскольку зачастую неадекватно описывают ситуацию. Например, два действия, характеризуемые одинаковым математическим ожиданием выигрыша, для ЛПР могут не быть равноценными. Поэтому далее будем рассматривать субъективный подход к принятию решений при риске. Среди методов этого подхода наиболее распространены и обоснованы те, которые опираются на аксиоматические построения: предпочтения формализуются с помощью некоторой модели, и формулируются условия, обеспечивающие ее существование. Важным направлением в развитии таких методов служит теория полезности, основанная на представлении структуры предпочтений ЛПР посредством одной или нескольких вещественных функций.

Необходимые сведения из теории полезности

Впервые условия, необходимые и достаточные для представления предпочтений ЛПР на множестве вероятностных мер с помощью линейной вещественно значимой функции, так называемой функции полезности, были получены Нейманом и Моргенштерном в 1947 году. В настоящее время принято разделять эти условия на две группы.

Условия из первой группы касаются множества всех рассматриваемых вероятностных мер и в современной литературе просто включаются в определение этого множества, называемого множеством вероятностных смесей. Вторая группа условий касается описания отношения предпочтения на множестве смесей - именно она известна сейчас как система аксиом Неймана-Моргенштерна, или аксиом классического представления полезности. Оценивается лотерея L:

р(А) + (1 -р)(В),

где А - выигрыш с вероятностью р, В - выигрыш с вероятностью (1- р).

Чтобы определить величину полезности, отражающую отношение индивида к какому-либо выигрышу X, мы его спрашиваем или наблюдаем за его поведением; в этом случае мы устанавливаем, при какой вероятности 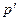ему безразлично, что выбрать - стандартный лотерейный билет L (p')или X. Оценка полезности U сводится к определению полезности U (L (p'))на основе выражения, сформулированного Нейманом и Моргенштерном. Кроме того, Нейман и Моргенштерн постулировали пять аксиом, достаточных, чтобы гарантировать существование такой функции полезности, при которой ранжирование лотерей по их ожидаемой полезности полностью соответствует действительным предпочтениям индивида.

Дата добавления: 2015-09-02