Схема применения метода интервалов для дробно-рациональной функции

Материал для подготовки к зачёту по математике 0

Некоторые сведения из теории

Схема применения метода интервалов для дробно-рациональной функции

Пусть дробно-рациональная функция, т. е. .

Рассмотрим метод интервалов для неравенств вида , , , .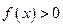

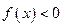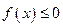1. Раскладываем многочлены 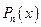и 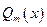на произведение линейных множителей и квадратичных множителей, для которых не существует действительных корней. Одинаковые корни объединяем.

2. На числовой прямой отмечаем область определения функции .

Замечание 1. Функция не существует в точках, где многочлен 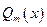обращается в нуль.

3. На этой числовой прямой отмечаем нули функции , которые совпадают с нулями функции 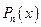. (Нули функции разбивают область определения на промежутки, на каждом из которых функция сохраняет знак).

4. Находим знаки функции в полученных промежутках.

Замечание 2. Для определения знака функции на конкретном промежутке можно найти её знак в любой (удобной) точке , принадлежащей этому промежутку.

Замечание 3. Если числитель 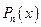или знаменатель 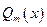содержат множитель 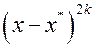(кратность корня четная), то при переходе через точку функция знак не меняет.

Замечание 3. Если числитель 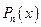или знаменатель 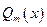содержат множитель 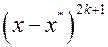(кратность корня нечетная), то при переходе через точку функция меняет знак на противоположный.

1. Записываем ответ.

Дата добавления: 2015-09-02