Лабораторная работа № 2. Исследование характеристик системы с очередями

2.1. Цель работы

Изучить характеристики систем массового обслуживания с очередями как модели системы временной коммутации и ознакомиться с вероятностной природой явлений, положенных в основу функционирования таких систем.

Перед выполнением лабораторно-практических заданий студенты должны обладать знаниями в области теории вероятностей и теории графов, знать преобразования Лапласа, пути решения систем линейных дифференциальных и алгебраических уравнений.

В результате выполнения лабораторно-практических заданий студенты должны освоить принципы расчета пропускной способности временного коммутатора на примере модели системы с очередями и оценивать среднюю длину очереди сообщений.

2.2. Краткие теоретические сведения

Рассмотрим СМО с очередями, состоящую из n устройств. В отличие от СМО с отказами, поступивший запрос, если устройства заняты, не получает отказа, а становится в очередь. Пусть N (t) -число устройств, занятых в момент времени t обслуживанием заявок; N (t) -случайный процесс с конечным множеством значений и непрерывным временем. Будем считать его однородной цепью Маркова. Пусть p_k(t) = P{N(t) = k} -вероятность того, что в момент времени t в СМО находится ровно k заявок, т.е. p_k(t) -одномерные законы распределения процесса N(t). Число k может принимать значения 0, 1, 2,..., n, n+1,... Если n ≥ k, это означает, что в СМО k устройств занято и очереди нет, если k > n, то все устройства заняты обслуживанием и k - n заявок стоят в очереди.

Не ограничивая длины очереди, рассмотрим только те характеристики СМО, которые не зависят от принципа отбора заявок из очереди.

Используя теорию однородных марковских цепей, теорию графов, систему дифференциальных уравнений Колмогорова–Чемпена и преобразование Лапласа, в итоге можно получить для вероятностей р_к формулу, которая называется формулой Эрланга для СМО с очередями:

и определим p₀ из условия нормировки:

Условие нормировки удовлетворяется в том случае, если ряд в левой части последнего равенства сходится. Этот ряд является геометрическим рядом и сходится, если α/n< 1, т.е. α < n.

Если α/n≥ 1, то геометрический ряд расходится и стационарного режима в СМО не существует, так как число заявок в очереди неограниченно возрастает.

В этом случае: ,

откуда

Формула Эрланга получена в предположении, что на вход СМО действует пуассоновский входной поток, а время обслуживания заявок распределено по показательному закону.

Основные важные характеристики системы с очередями, получаемые на основе формулы Эрланга, в литературе называются основными формулами Эрланга и сведены в табл. 2.1 (см. ниже).

2.3. Лабораторное задание

1. На специализированный факс-сервер узла телекоммуникационных услуг отправили факс-сообщение, причем плотность нагрузки составляет α. Определить зависимость средней длины очереди m от числа каналов специализированного сервера.

Лицевая панель виртуального прибора показана на рис. 2.1, диаграммная панель, в соответствии с формулами для расчета средней длины очереди, приведена на рис.2.2.

2. На вход системы временной коммутации, имеющей n каналов, поступает пуассоновский входной поток с плотностью λ запросов в минуту. Определить зависимость средней длины очереди m от интенсивности обслуживания.

3. На вход n -канальной системы временной коммутации поступает пуассоновский входной поток запросов. Определить зависимость средней длины очереди m от плотности входного потока λ, если известно, что плотность нагрузки может изменяться от α_min до α_max.

Таблица 2.1 Формулы Эрланга для системы с очередями

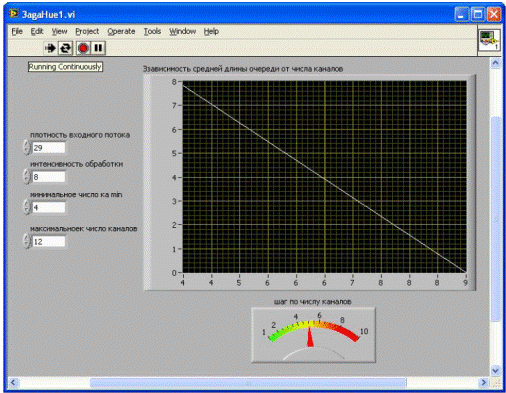
Рис.2.1. Примерный вид зависимости величины средней длины очереди от числа каналов.

Рис.2.2. Примерный вид зависимости средней длины очереди от интенсивности обслуживания

Рис.2.3. Примерный вид зависимости величины средней длины очереди от плотности нагрузки

2.4 Контрольные вопросы

1. Принцип коммутации сообщений.

2. Принцип коммутации пакетов.

3. Что такое СМО с очередями?

4. Привести и пояснить формулу Эрланга для СМО с очередями.

5. Что такое плотность нагрузки СМО?

6. Привести формулу для нахождения вероятности того, что все каналы в системе с очередями заняты.

6. Пояснить, при каких условиях не будет наблюдаться бесконечного возрастания длины очереди.

7. Что такое текущая длина очереди и средняя длина очереди?

8. Привести формулу для средней длины очереди.

9. От каких параметров и как зависит средняя длина очереди?

10. От каких параметров и каким образом зависит вероятность того, что в СМО с очередями нет очереди?

11. От чего и как зависит вероятность того, что заявка на обслуживание в СМО с очередями не будет сразу же принята на обслуживание?

12. На почтовый сервер узла сети поступает поток заявок на отправку электронной корреспонденции – в среднем N писем в Δt минут. Среднее время обработки одной заявки составляет Т минут. Определить, сколько нужно иметь каналов для того, чтобы с вероятностью Р₀ на почтовом сервере не создавалась очередь?

Дата добавления: 2015-09-02