Найти площадь фигуры, ограниченной линиями , .

Вычислить интеграл.

Решение.

Сделаем замену √x = t, тогда:

x = t² ,

dx = 2*t*dt, преобразуем в виде неопределенного интеграла:

{ S – это вместо знака интеграла, т.к. я не знаю Word)) }

S ( t*sin(t)*2*t*dt) = S ( 2*t²*sin(t)*dt) = (1),

Проведем интегрирование по частям, представив (1) в виде:

S u*dv= u*v - S v*du,

Где u = 2*t², dv = sin(t)*dt, тогда:

(1) = 2*t² *(-cos(t)) - S ( -cos(t)*4*t*dt) = 2*t² *(-cos(t)) + 4*S ( cos(t)*t*dt),

Представим S ( cos(t)*t*dt) в виде:

S u*dv= u*v - S v*du,

Где u = t, dv = cos(t)*dt, тогда:

S ( cos(t)*t*dt) = t*sin(t) - S sin(t)*dt = t*sin(t) +cos(t)+C, тогда (1) запишем в виде:

(1) = 2*t² *(-cos(t)) + 4*(t*sin(t) +cos(t)) + С = -2* t² *cos(t)+ 4*t*sin(t)+

+4* cos(t) + С,

Сделаем замену t=√x, и введем пределы интегрирования для x, тогда:

│₀ ^п2 (-2* t² *cos(t)+ 4*t*sin(t)+4* cos(t)) =

= (-2* п² *cos(п)+4*п*sin(п)+4* cos(п)) - (-2* 0*cos(0)+4*0*sin(0)+4* cos(0))= = (2* п² + 0 – 4) – (0 + 0 +4) = 2* п² - 8.

Найти площадь фигуры, ограниченной линиями,.

Решение.

Приравняем функции друг к другу и найдем точки пересечения этих функций:

27/(х²+9) = х² /6, преобразуем:

(х²+9)*х² = 6*27,

х⁴ + 9*х² – 162 = 0,

Пусть х² = т, т≥0, тогда:

т² +9*т–162 = 0, решаем:

корни уравнения т1= 9, т2 = -18, второй корень не подходит по условию т≥0, тогда

т = 9, а т = х², значит х² = 9, корни уравнения х1 = 3, х2 = -3,таким образом точки пересечения 2-х функций х1 = 3, х2 = -3.

Найдем площадь фигуры как интеграл по пределам интегрирования:

S_-3³((27/(х²+9) - х² /6)*dx) = S_-3³((27*6- х²*(х²+9))/((х²+9)*6)*dx) =

= S_-3³(1/6*((162* dx)/(х²+9) – х²*(х²+9)*dx/(х²+9))) =

= S_-3³(1/6*((162* dx)/(х²+9) – х²*dx)) =

= 1/6*│_-3³ (162*(1/3*arctg(x/3)) – 1/3*x³) =

= 1/6* ((162*(1/3*arctg(3/3)) – 1/3*3³) - (162*(1/3*arctg(-3/3)) – 1/3*(-3)³))=

= 1/6* ((162*(1/3*п/4) – 9) - (162*(1/3*(-п/4)) + 9))=

= 1/6* (27*п/2 – 9 + 27*п/2 - 9)= 1/6*(27*п – 18) = (9/2*п – 3) квадратных единиц.

8. Найти частное решение дифференциального уравнения
.

Решение:

Преобразуем уравнение.

y’/(2y – 1) = tg x/cos² x, y’ = dy/dx, то

(dy/dx) /(2y – 1) = tg x/cos² x

dy /(2y – 1) = dx*tg x/cos² x

Интегрируем уравнение:

1)S dy /(2y – 1) = S 1/2 * d(2y – 1) /(2y – 1) = 1/2 * ln(2y – 1) + C1,

2)S dx*tg x/cos² x = 1/2 * tg² x + C2,

Приравняем 1 и 2 части уравнения:

1/2 * ln(2y – 1) + C1 = 1/2 * tg² x + C2,

ln(2y – 1) = tg² x + C3,

2y – 1 = e^(tg² x + C3),

2y – 1 = C4* e^(tg² x),

y= C* e^(tg² x) + 1/2,

Если y(0) = 1, то

1 = C*e^(tg²0) + 1/2,

1 = C*e^0 + 1/2,

1 = C*1 + 1/2,

C = 1/2, значит

y= 1/2* e^(tg² x) + 1/2.

Проверка:

1. Если х=0, то у = 1/2* e^(tg² 0) + 1/2 = 1/2* e^0+ 1/2 = 1/2 + 1/2= 1. Верно.

2. y’= (1/2* e^(tg² x) + 1/2)’ = (tg² x)’*1/2*e^(tg² x)=

= (tg x)’*1/2* 2*tg x *e^(tg² x) = (1/cos²x)*1/2* 2*tg x *e^(tg² x).

Подставим y и y’ в уравнение:

(1/cos²x)*1/2* 2*tg x *e^(tg² x) *cos² x = (2*(1/2*e^(tg² x) + 1/2) –1)*tg x,

tg x *e^(tg² x) = e^(tg² x) * tg x. Верно.

Ответ: y= 1/2* e^(tg² x) + 1/2.

9. Найти общее решение дифференциального уравнения
.

Решение.

Разделим обе части уравнения на х ≠ 0:

у’ – у/х = 1 /(cos (у/х)), пусть y=t*x, то у’= t+t’x,

t =2*п*к,

t + t’x – t*x/x = 1/(cos(t*x/x)),

t + t’x – t = 1/cos(t),

t’x = 1/cos(t),

dt/dx*x*cos(t) = 1,

dt*cos(t) = dx/x

Возьмем интегралы обеих частей уравнения:

S cos(t)*dt =sin(t) = sin(y/x),

S dx/x = ln(x) + lnC = ln(C*x),

Приравняем:

Sin(y/x) = ln(C*x),

Ответ: Sin(y/x) = ln(C*x); t =2*п*к.

10. Найти частное решение дифференциального уравнения
.

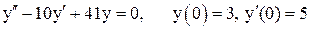Решение.

Составим и решим характеристическое уравнение.

λ² - 10 λ + 41 = 0, найдем дискриминант:

D = (10)² – 4*41 = -64, D<0, √D = ±8i,

Найдем корни уравнения:

λ1 = (10 + 8i)/2 = 5 + 4i,

λ2 = (10 - 8i)/2 = 5 - 4i,

Общее решение уравнения:

y = (e^(5x)) * (C1*cos 4x + C2*sin 4x),

Найдем y’:

y’= (e^(5x)) * (C1*cos 4x + C2*sin 4x)’ +

(e^(5x))’ * (C1*cos 4x + C2*sin 4x) =

= (e^(5x)) * (-C1*4*sin 4x + C2*4*cos 4x) +

+ (5*e^(5x)) * (C1*cos 4x + C2*sin 4x) =

= (e^(5x))*(-C1*4*sin 4x + C2*4*cos 4x + 5*C1*cos 4x + 5*C2*sin 4x) =

= (e^(5x))*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5* sin 4x)).

Если y(0) = 3, то

3 = (e^(5*0)) * (C1*cos 4*0 + C2*sin 4*0),

3 = (e^0) * (C1*cos 0 + C2*sin 0),

3 = 1 * (C1*1 + C2*0),

C1 = 3.

Если y’(0) = 5, то:

5= (e^(5*0))*(3*(5*cos 4*0 - 4*sin 4*0) + C2*(4*cos 4*0 + 5* sin 4*0)).

5= (e^0)*(3* (5-0) + C2*(4+0)),

5= 1*(15 + 4*C2),

4*C2 = -10,

C2 = -2,5.

Частное решение дифференциального уравнения:

y = (e^(5x)) * (3*cos 4x -2,5*sin 4x),

Проверка:

1. y(0) =3, то

3= (e^(5*0)) * (3*cos 4*0 -2,5*sin 4*0),

3= 1*(3 -0),

3= 3, верно.

2. y’(0) =5, то

5 = (e^(5*0))*(3*(5*cos 4*0 - 4*sin 4*0) -2,5*(4*cos 4*0 +

+5* sin 4*0)).

5 = 1*(15 - 10).

5= 5, верно.

3. Возьмем y’’.

y’’ = ((e^(5x))*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5*sin 4x)))’.

y’’ = (e^(5x))*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5*sin 4x))’+

+ (e^(5x))’*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5*sin 4x)).

y’’ = (e^(5x))*(C1*(-5*4*sin 4x - 4*4*cos 4x)+C2*(-4*4*sin 4x + 5*4*cos 4x))+

+ (5*e^(5x))*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5*sin 4x)).

y’’ = (e^(5x))*(C1*(-20*sin 4x - 16*cos 4x)+C2*(-16*sin 4x + 20*cos 4x))+

+ (5*e^(5x))*(C1*(5*cos 4x - 4*sin 4x) + C2*(4*cos 4x + 5*sin 4x)).

y’’ = (e^(5x))*(C1*(-20*sin 4x - 4*cos 4x)+C2*(-16*sin 4x + 20*cos 4x))+

+ (e^(5x))*(5*C1*(5*cos 4x - 4*sin 4x) +5* C2*(4*cos 4x + 5*sin 4x)).

y’’ = (e^(5x))*(C1*(-20*sin 4x - 16*cos 4x)+C2*(-16*sin 4x + 20*cos 4x))+

+ (e^(5x))*(C1*(25*cos 4x - 20*sin 4x) +C2*(20*cos 4x + 25*sin 4x)).

y’’ = (e^(5x))*(C1*(-20*sin 4x - 16*cos 4x+25*cos 4x - 20*sin 4x)+

+C2*(-16*sin 4x + 20*cos 4x+20*cos 4x + 25*sin 4x)),

y’’ = (e^(5x))*(C1*(-40*sin 4x +9*cos 4x)+C2*(40*cos 4x+ 9*sin 4x)),

Упростим выражения y, y’, y’’, подставив числовые значения коэффициентов C1 и C2:

y= (e^(5x)) * (3*cos 4x -2,5*sin 4x),

y’= (e^(5x))*(3*(5*cos 4x - 4*sin 4x) -2,5*(4*cos 4x + 5* sin 4x))=

=(e^(5x))*(15*cos 4x - 12*sin 4x -10*cos 4x -12,5* sin 4x)=

=(e^(5x))*(5*cos 4x – 24,5*sin 4x),

y’’= (e^(5x))*(3*(-40*sin 4x +9*cos 4x)-2,5*(40*cos 4x+ 9*sin 4x))=

= (e^(5x))*(-120*sin 4x +27*cos 4x-100*cos 4x-22,5*sin 4x)=

= (e^(5x))*(-142,5*sin 4x -73*cos 4x),

Подставим y, y’, y’’ в левую часть уравнения y’’ –10y’+41y=0:

(e^(5x)) *(-142,5*sin 4x -73*cos 4x) – 10*(e^(5x))*(5*cos 4x – 24,5*sin 4x)+

+41*(e^(5x))* (3*cos 4x -2,5*sin 4x) = 0,

(e^(5x))*(-142,5*sin 4x -73*cos 4x - 50*cos 4x + 245*sin 4x+

+123*cos 4x – 102,5* sin 4x) = 0,

-142,5*sin 4x -73*cos 4x - 50*cos 4x + 245*sin 4x+

+123*cos 4x – 102,5* sin 4x = 0,

(-142,5 +245 – 102,5)*sin 4x + (-73 – 50 + 123)*cos 4x = 0,

0*sin 4x + 0*cos 4x = 0,

0 = 0, верно.

Ответ: y = (e^(5x)) * (3*cos 4x -2,5*sin 4x).

_______________________________________________

Дата добавления: 2015-09-01