Теплоемкость кристаллов

4.3.1 Закон Дюлонга и Пти

Атомы в твердом теле при любой температуре Т совершают тепловые колебания около своих средних положений равновесий. Если нагревать твердое тело, то поглощаемое им тепло расходуется на увеличение интенсивности теплового движения. Амплитуда колебаний атомов при умеренно высоких температурах растет пропорционально .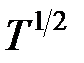

Говоря о теплоемкости, мы обычно будем иметь в виду теплоемкость при постоянном объеме 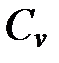, которая является более фундаментальной величиной, чем теплоемкость при постоянном давлении 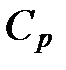, которую обычно определяют в экспериментах.

Основные особенности теплового движения в твердых телах можно понять, рассматривая поведение теплоемкости с изменением температуры. По определению, теплоемкость вещества, отнесенная к одному молю ― это энергия, которую необходимо сообщить молю вещества, чтобы повысить его температуру на 1º.

.

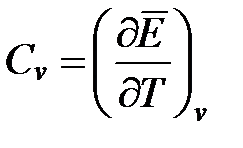В 1819 году французские ученые Дюлонг и Пти экспериментально установили закон, согласно которому удельная теплоемкость всех твердых тел, при достаточно высоких температурах, есть величина постоянная, не зависящая от температуры, и составляет около 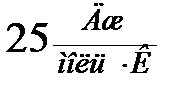, т.е. при нагревании любого твердого тела на 1º каждый его атом поглощает одно и тоже количество энергии.

Объяснение этому эффекту можно найти, исходя из известного закона равномерного распределения энергии по степеням свободы.

Средняя энергия системы, в соответствии с этим законом, равна произведению числа степеней свободы на 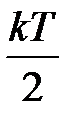– т.е. на каждую степень свободы приходится энергия, равная 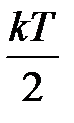(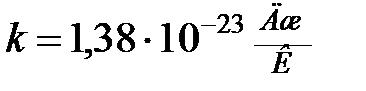). Этот результат, справедлив для идеальных газов, легко распространить на системы частиц, взаимодействующих между собой, и когда силы взаимодействия гармонические, т.е. подчиняются закону Гука.

В этом случае в качестве модели можно выбрать твердое тело, атомы которого совершают малые колебания около положений равновесия в узлах кристаллической решетки. Каждый атом, независимо от соседей колеблется в трех взаимно перпендикулярных направлениях, т.е. он имеет три независимые колебательные степени свободы. Такой атом можно уподобить совокупности трех линейных гармонических осцилляторов. При колебаниях осциллятора последовательно происходит преобразование кинетической энергии в потенциальную и потенциальной в кинетическую. Поскольку средняя кинетическая энергия, составляющая 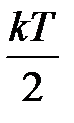на одну степень свободы, остается неизменной, а средняя потенциальная энергия точно равна средней кинетической, то средняя полная энергия осциллятора, равная сумме кинетической и потенциальной энергии, будет составлять:

.

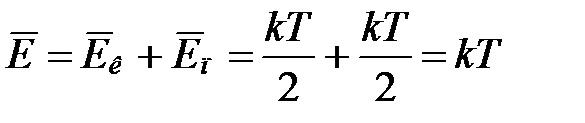Если кристалл состоит из атомов , то при наличии для каждого атома трех колебательных степеней свободы кристалл будет представлять собой систему с 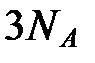степенями свободы. Тогда полная средняя тепловая энергия такой системы:

.

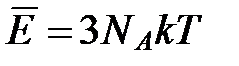Отсюда теплоемкость, как приращение энергии, соответствующей повышению температуры на 1º, будет равна:

. .

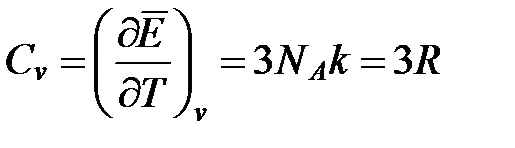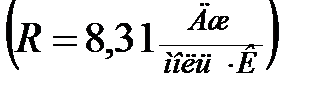Это соотношение называют законом Дюлонга и Пти. При высоких температурах этот закон довольно хорошо выполняется для многих твердых тел. Однако при низких температурах теплоемкость падает до нуля.

4.3.2 Модель Эйнштейна

Объяснение того, почему теплоемкость в действительности уменьшается при охлаждении, должно сводиться к объяснению причин, в силу которых средняя энергия, связанная с колебательной модой, зависит от температуры и ее частоты ω.

Первый успех в этой области связан с именем Эйнштейна, который основывался на разработанной Планком квантовой теории изучения черного тела. Согласно этой теории квантовый осциллятор, колеблющийся с частотой 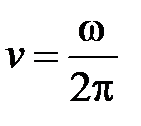, может находиться только в состоянии с энергией

,

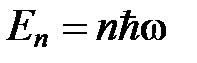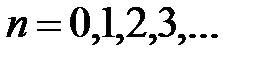
Вероятность пребывания в состоянии n равна:

.

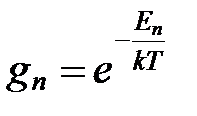Тогда средняя энергия этого осциллятора, находящегося в тепловом равновесии, определяется как

.

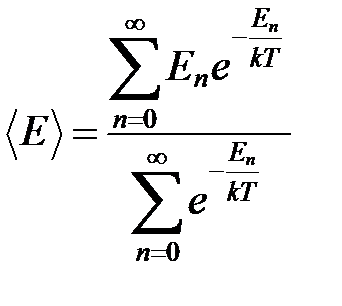В результате получаем для квантового гармонического осциллятора, колеблющегося с частотой ω:

.

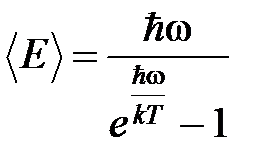Другой способ определения средней энергии состоит в вычисление среднего числа фотонов, соответствующего при температурах Т колебанием решетки с угловой частотой ω:

.

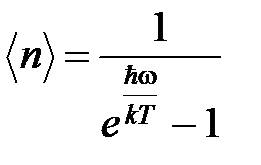Величины 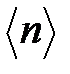называют числами заполнения данной моды.

Согласно принципам современной квантовой механики, разрешенные значения энергии квантового осциллятора равны 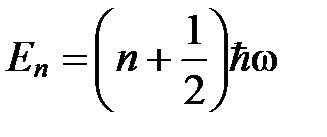, так что

. (1)

Дополнительная энергия 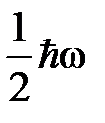для каждой моды представляет собой энергию нулевых колебаний, она названа так из-за того, что эта энергия существует при любой температуре, в том числе и при абсолютном нуле. Энергия нулевых колебаний, которая не зависит от температуры, автоматически входит в энергию решетки. Ее добавление к общей энергии не влияет на величину теплоемкости.

Эйнштейн отождествил кристаллическую решетку из N атомов с системой 3N независимых гармонических осцилляторов с одинаковой собственной частотой ω.

Существование нулевой энергии колебаний было установлено значительно позже, лишь после создания квантовой механики. Поэтому Эйнштейн исходил из планковского значения энергии гармонического осциллятора 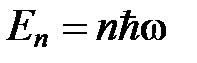. Соответственно в использованном Эйнштейном выражении для слагаемое 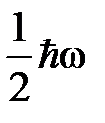отсутствовало.

Умножив второе слагаемое выражения (1) на 3N Эйнштейн получил для внутренней энергии кристалла формулу:

.

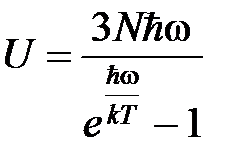Продифференцировав это выражение по температуре, Эйнштейн нашел теплоемкость кристалла:

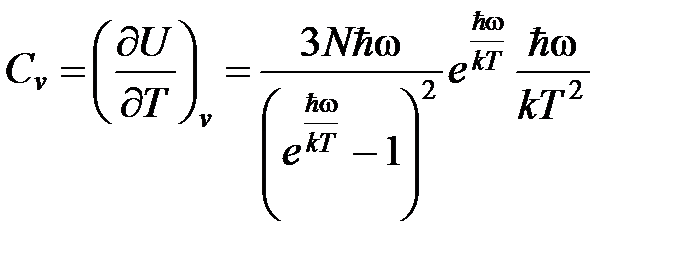. (2)

Рассмотрим два предельных случая.

1. Высокие температуры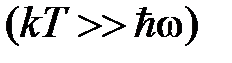

Разложим в ряд знаменатель выражения (2):

.

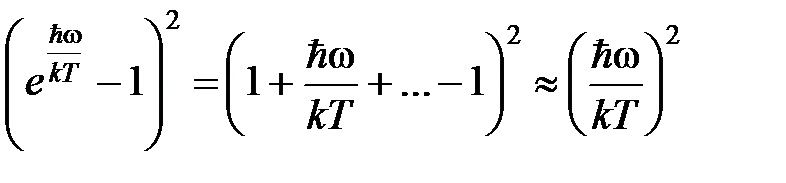В числителе 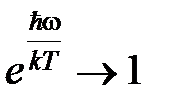, тогда:

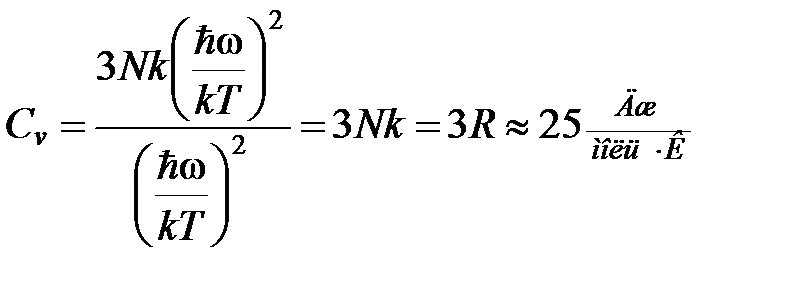
Т.е. при высоких температурах значение теплоемкости приводит к закону Дюлонга и Пти.

2. Низкие температуры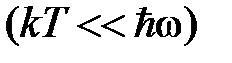

В этом случае в знаменателе единицей можно пренебречь, тогда:

.

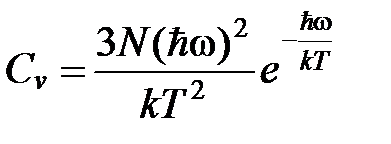Как следствие из этого выражения при стремлении температуры твердого тела к 0, экспоненциальный множитель оказывается преобладающим, так что теплоемкость стремится к 0 по закону 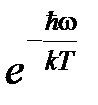(см. рис.).

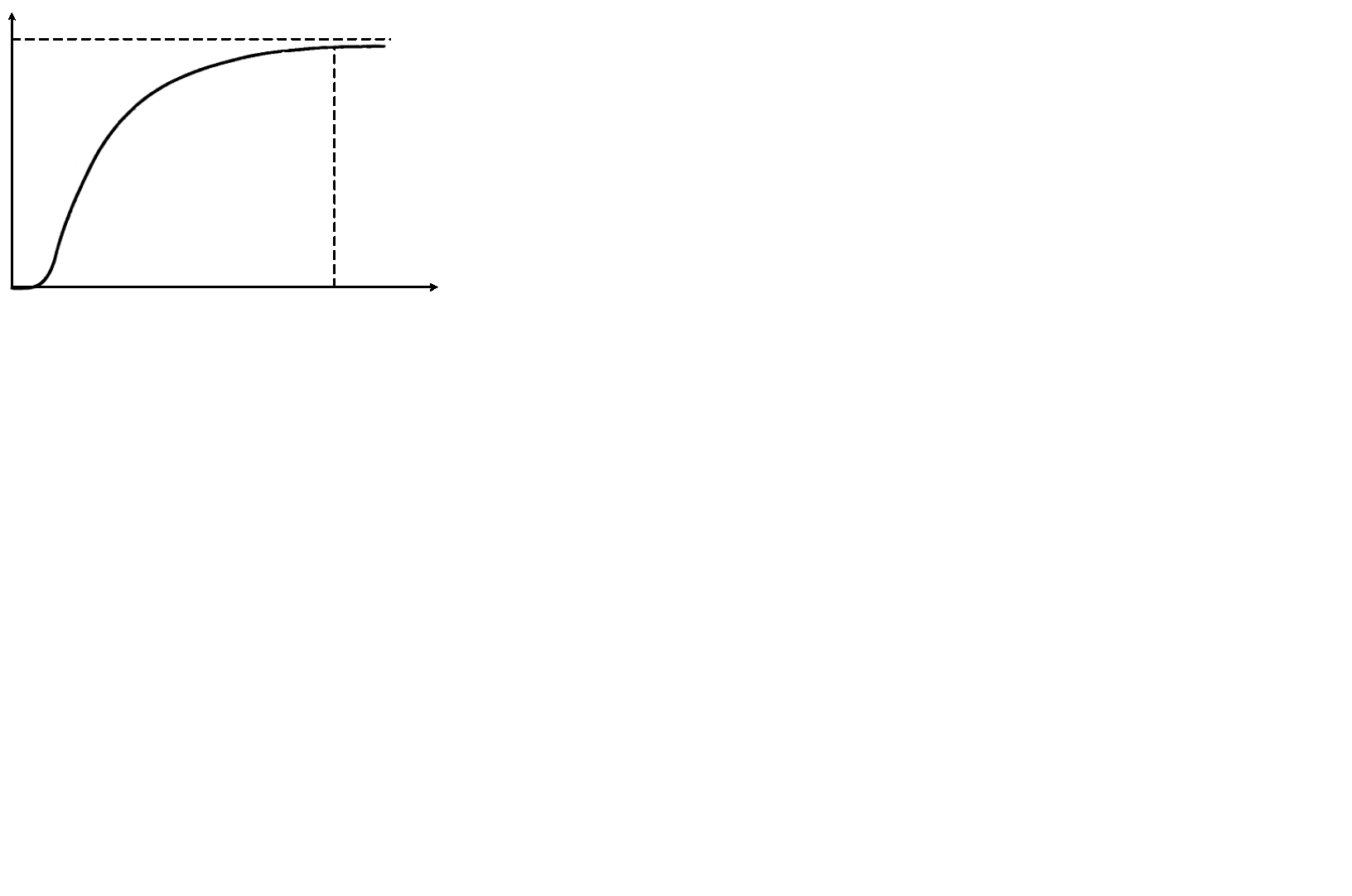
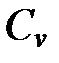
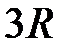
Рисунок – Удельная теплоемкость кристалла в приближении Эйнштейна

Основной причиной убывания теплоемкости является то, что при низких температурах закон равномерного распределения энергии по степеням свободы становится несправедливым.

Средняя энергия осциллятора 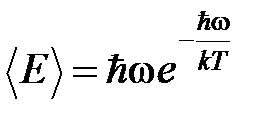при 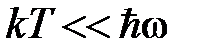экспоненциальн обыстро падает до 0 при температуре, стремящейся к 0, в то время как в соответствии с законом равномерного распределения она падает до нуля линейно. Таким образом, модель Эйнштейна действительно хорошо описывает факт резкого уменьшения теплоемкости при низких температурах при надлежащем подборе частоты осциллятора ω.

Температура, при которой начинается быстрый спад теплоемкости и получившая название характеристической температуры Эйнштейна 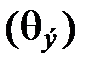, очевидно, определяется близостью к :

,

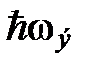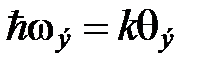если положить 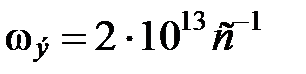; ; 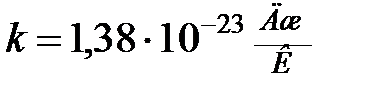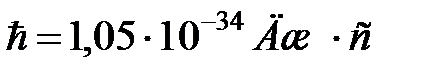, то .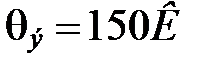

Реальная температура Эйнштейна зависит от свойств веществ, для большинства твердых тел она порядка 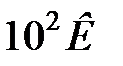, но есть вещества(бериллий, алмаз), у которых 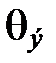аномально высока (выше 1000 К).

Характеристическая температура 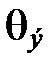является одной из важнейших характеристик кристалла. При температурах ниже характеристической 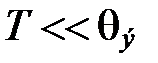необходимо квантовое рассмотрение.

При 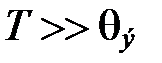квантование энергии можно не учитывать и рассмотрение вести исходя из обычных классических представлений.

4.3.3 Модель Дебая

Дебай учел, что колебания атомов в кристаллической решетке не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение других соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных друг с другом атомов, обладающую 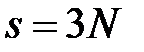степенями свободы.

Произвольное колебание струны является суперпозицией гармонических стоячих волн. Следовательно, каждое нормальное колебание струны представляет собой стоячую волну.

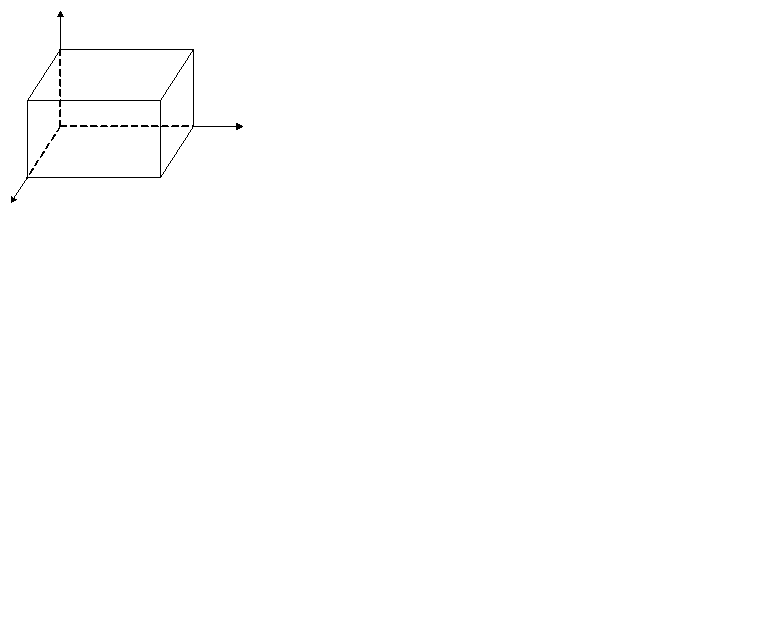
Аналогично, каждому нормальному колебанию кристаллической решетки соответствует стоячая волна, устанавливающаяся в объеме кристаллического тела. Действительно, из-за связи между атомами колебание, возникающее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Дойдя до границы кристалла, волна отражается. При положении прямой и отраженной волн образуется стоячая волна. Стоячие волны могут возникать для частот(или длин волн), удовлетворяющих определенным условием. Если взять кристаллическое тело в виде параллелепипеда со сторонами a, b, c (см. рис.), то эти условия выражаются формулами:

,

,

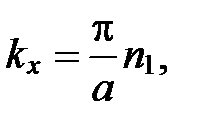
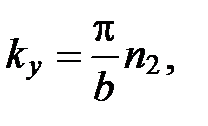
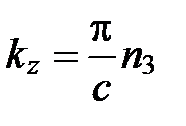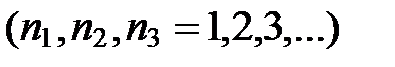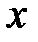
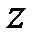
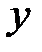
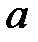
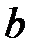
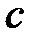
где 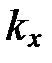, , 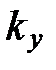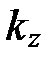― проекции волнового вектора по оси x, y, z.

Число стоячих волн, т.е. нормальных колебаний, частоты которых заключены в интервале от ω до ω+ d ω, определяется выражением:

,

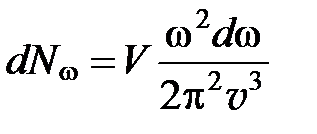где 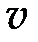― фазовая скорость волны в кристалле.

Объем кристалла V входит в это выражение в виде отдельного множителя. Поэтому можно говорить о числе нормальных колебаний, приходящихся на единицу объема кристалла:

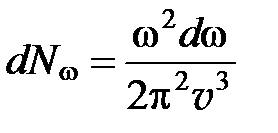. (3)

Данная формула не учитывает возможных видов поляризации волны. В твердой среде вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением ω, отличающиеся направлением поляризации: одна продольная и две поперечные с взаимно перпендикулярными направлениями колебаний.

В соответствии с этим значением запишем формулу (3) нужно видоизменить следующим образом:

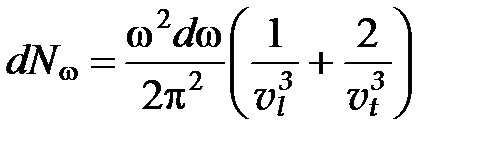, (4)

где 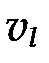― фазовая скорость продольных волн, а 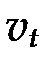― фазовая скорость поперечных упругих волн. Положим для простоты, что .

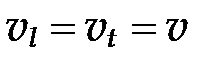Тогда

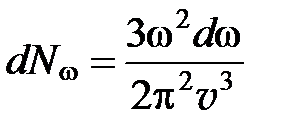. (5)

Максимальную частоту ω _m нормальных колебаний решетки можно найти, приравняв полное число колебаний к числу степеней свободы, равному 3 n (n ― число атомов в единице объема кристалла):

.

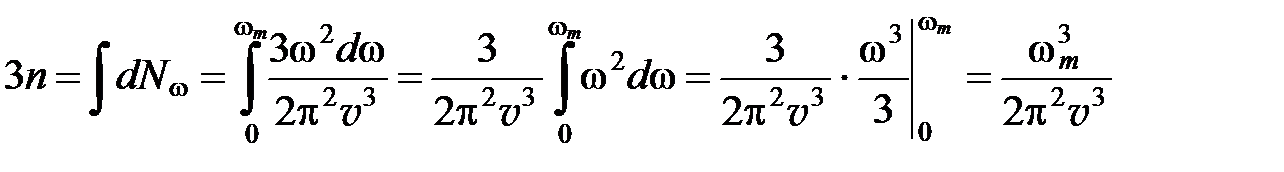Отсюда:

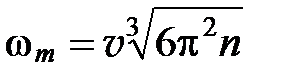. (6)

Тогда наименьшая длина волны, возбуждаемая в кристалле равна:

,

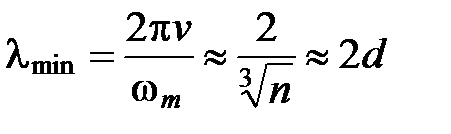где d ― расстояние между соседними атомами в решетке. Этот результат согласуется с тем, что волны, длина которых меньше удвоенного межатомного расстояния, не имеют физического смысла.

Исключим из равенств (5) и (6) скорость :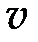

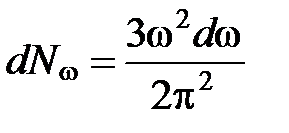. (7)

,

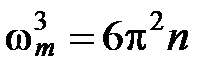
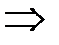
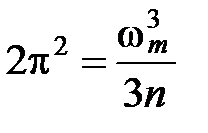подставим 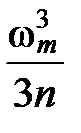в выражение (7), и получим для числа нормальных колебаний 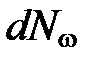в интервале частот 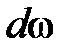, приходящегося на единицу объема кристалла, следующее выражение:

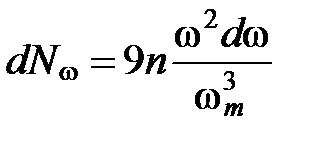. (8)

Внутренняя энергия единицы объема кристалла может быть представлена в виде:

,

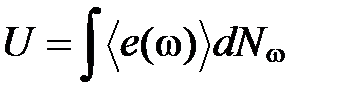где 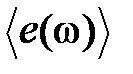― среднее значение энергии нормального колебания частоты ω. Подставив выражение 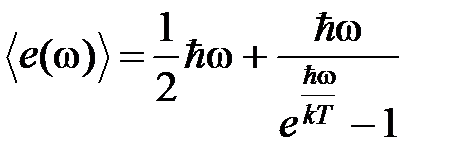и (8) для 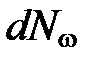, придем к формуле:

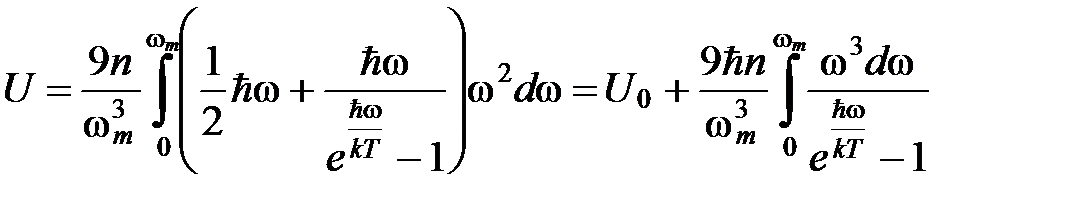. (9)

Здесь 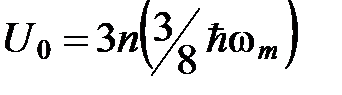― энергия нулевых колебаний кристалла.

Производная от U по T дает теплоемкость единицы объема кристалла:

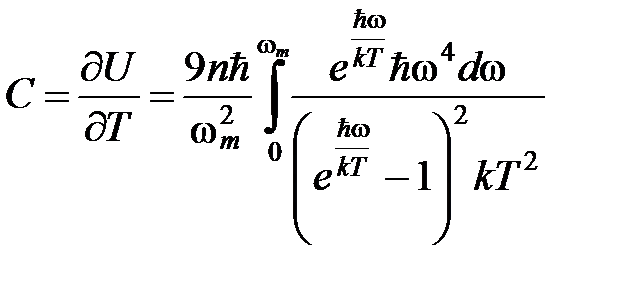
Величину θ, определяемую условием: 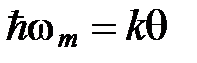, называют характеристической температурой Дебая. По определению,

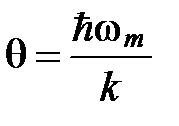. (10)

Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний.

Введем переменную 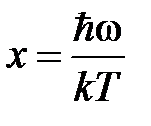, 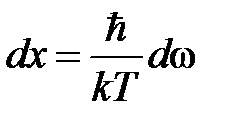. Тогда выражение для теплоемкости примет вид

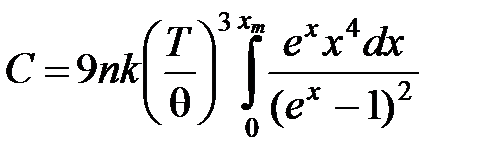, (11)

где .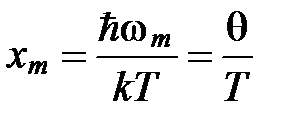

1. Случай низких температур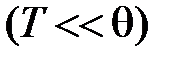

Верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности 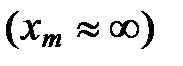.Тогда интеграл будет представлять собой некоторое число, и теплоемкость С окажется пропорциональной кубу температуры, ~ 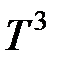. Эта приближенная зависимость известна как закон кубов Дебая. При достаточно низких температурах закон выполняется во многих случаях очень хорошо.

2. Случай высоких температур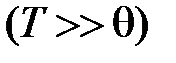

При 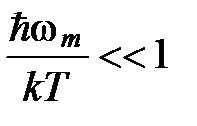, формулу (9) можно упростить, положив 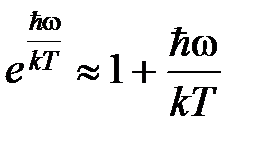. Тогда для внутренней энергии получается выражение

,

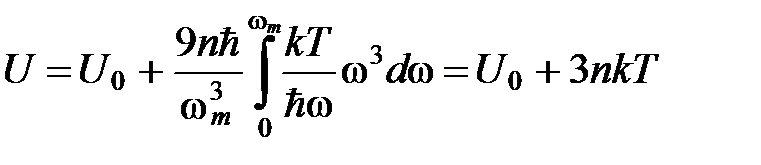а для теплоемкости значение 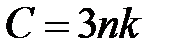, фигурирующее в законе Дюлонга и Пти.

О согласии теории Дебая с опытом можно судить по рисунку, на котором приведены данные для теплоемкости алюминия 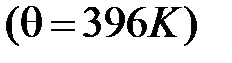и меди 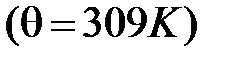; ― классическое значение теплоемкости, получающиеся из квантовых формул при 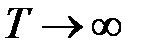. Кривые построены по формуле (11), кружками показаны экспериментальные точки.

Рисунок

Формула Дебая хорошо передает ход теплоемкости с температурой лишь для тел с простыми кристаллическими решетками, т.е. для химических элементов и некоторых простых соединений.

К телам с более сложной структурой формула Дебая неприменима. Это вызвано тем, что у таких тел спектр колебаний оказывается чрезвычайно сложным.

Дата добавления: 2015-09-01