Системи числення

Вступ

Комп’ютерна схемотехніка відноситься до числа найбільш важливих курсів для підготовки сучасних фахівців – електриків, електромеханіків, електроенергетиків, комп’ютерників та фахівців інших електротехнічних спеціальностей. Комп’ютерна схемотехніка охоплює широкий розділ науки і техніки, який пов’язаний з вивченням арифметичних і логічних основ схемотехніки, на базі яких функціонують різноманітні електронні пристрої.

За допомогою домашнього завдання майбутні спеціалісти закріплюють матеріал: арифметичні і логічні основи комп’ютерної схемотехніки, а саме правила виконання операцій у комп’ютерній схемотехніці над двійковими числами і правила складання робочих функцій комбінаційних вузлів схемотехніки і побудови схем на логічних елементах.

1 ЗАГАЛЬНІ ВІДОМОСТІ

Мета: Закріплення та експериментальне підтвердження теорети­чного матеріалу по системам числення, по способам мінімізації булевих функційта принципу функціонування мікропроцесорів.

Порядок виконання роботи

- Виконати практичну частину роботи. Завдання наведено у п. 1.4.

- Оформити звіт. Вимоги до оформлення звіту наведені у п.1.6. Титульний аркуш наведено у додатку В.

1.2 Рекомендована література: [5],с. 5-25, 100-128.

Теоретичні відомості

Системи числення

Системою числення називається сукупність цифр і правил для запису чисел. Запис числа в деякій системі числення називається його кодом.

Система числення з основою два (цифри 0 й 1) називається двійковою, система числення з основою три (цифри 0, 1,2) —трирічною т.д. У системах числення з основою менше десяти використовують десяткові цифри, а для основи більше десяти додають букви латинського алфавіту — А, В, З, D, E, F.

Таблиця 1.1 – Типи систем числення

Основа q	Система числення	Знаки
	Двійкова Трирічна П’ятирічна Восьмерична Десяткова Шістнадцятирічна	0,1 0, 1,2 0,1,2,3,4 0,1,2,3,4,5,6,7 0, 1,2, 3,4,5, 6, 7, 8, 9 0, 1,2, 3,4, 5, 6, 7, 8, 9, А,В,З,D,E,F

Число в позиційній системи можна представити поліномом:

(1.1)

де q – основа системи числення;

qⁱ - вага позиції;

- цифри в позиціях числа;

0, 1,.... до — номера розрядів цілої частини числа;

-1, -2,…,- m –номер розрядів дробової частини числа.

Приклад 1.1

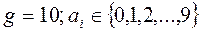Ілюстрація запису чисел у вигляді послідовності цифр (1.1) і відповідного полінома: · двійкова система: : · восьмирічна система: : · десяткова система: : · шістнадцятирічна система: :  

Розглянуті записи чисел показують один зі способів перекладу не десяткових чисел у десяткові. При однаковій розрядності в системах числення з більшою основою можна записати більше різних чисел.

Перевагами двійкової системи є: простота виконання арифметичних операцій; наявність надійних мікроелектронних схем із двома стійкими станами (тригерів), призначених для зберігання значень двійкового розряду — цифр 0 або 1. Двійкові цифри називають також бітами. У двійково-десятковій системі числення кожна десяткова цифра записується чотирма двійковими розрядами (тетрадами).

Приклад 1.2

Запис десяткового числа у двійково-десятковій системі:

(1.2)

У формі із плаваючою комою числа представляються у вигляді добутків:

де q — підстава системи числення (звичайно цілий ступінь числа 2);

П — порядок числа довжиною k +1 (ціле число зі знаком);

М — мантиса числа довжиною r +1 (правильний дріб зі знаком);

X — характеристика числа.

Приклад 1.3

Ілюстрація запису числа у формі із плаваючою комою:  

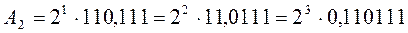
Додатні числа у всіх кодах записуються однаково. Якщо позначити машинні зображення числа А в прямому коді [ А ]_ПР, у зворотному коді [ A ] _ЗВ, у додатковому коді [ А ]_ДОД, то для додатних чисел маємо:

Для від’ємних чисел у знаковому розряді через кому ставиться одиниця, а для додатних - нуль:

Приклад 1.4

Запис двійкових чисел А = 1010₂ й В = -1010₂ у прямих кодах: [А]_ПР = 0,1010; [В]_ПР= 1,1010.

Зворотний код від’ємного числа утворюється з його прямого коду після інвертування значень розрядів цифрової частини, тобто заміною нуля на одиницю й одиниці - на нуль; значення знакового розряду не змінюється. Додатковий код негативного двійкового числа утворюється з його зворотного коду шляхом додавання одиниці до молодшого розряду.

Приклад 1.5

Подання у зворотному й додатковому кодах двійкових чисел: цілого А = -1001₂ і дробового В = -1001₂:

Для переходу від зворотного коду негативного числа до прямого коду потрібно інвертувати значення розрядів цифрової частини, не змінюючи значення знакового розряду. Для переходу від додаткового коду негативного числа до прямого спочатку одержують його зворотний код, а потім додають одиницю до молодшого розряду.

Правила виконання операцій додавання, вирахування, множення й додавання по модулі 2 у двійковій арифметиці представлені в таблиці 1.2. При додаванні двох одиниць виникає перенос у старший розряд; при вирахуванні з нуля одиниці потрібен позика зі старшого розряду.

Таблиця 1.2 – Правила двійкової арифметики

Дата добавления: 2015-09-01