
Читайте также:
|
Однако, как в случае аристотелевской, так и в случае любых разновидностей традиционной силлогистики фундаментальным для понимания смысла простых категорических атрибутивных высказываний оказывается логическое отношение их терминов, т. е. выступающих в роли субъекта и предиката разных по объёму, соединённых предицирующими связками имён. Те отношения между терминами высказываний, которые в случае каждой формы отвечают условию истинности, получили название модельных схем.
Модельные схемы фиксируют «объём сказывания» (мыслимое в высказывании положение дел). Объём сказывания наглядно выявляется посредством совмещения: 1) объёма «универсума» (что характерно для традиционной силлогистики), обозначаемого четырёхугольником c латинской «U», 2) объёма субъекта, (так называемая «круговая схема» или «круг Эйлера») с латинской «S» и 3) объёма предиката, обозначаемого вторым кругом Эйлера с латинской «P». Объём сказывания может быть нулевым, когда субъект и предикат суждения не имеют ни одного общего элемента, и ненулевым, который фиксируется на модельных схемах штриховкой, покрывающей общие у субъекта и предиката элементы.
Для общеутвердительных (A) суждений существуют только две модельные схемы (рис. 4):
I II
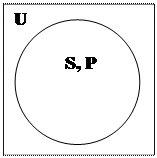 | 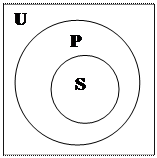 |
Рис. 4
Первая схема фиксирует штриховкой объём сказывания при наличии между S и P отношения равнозначности (тождественности), т. е. когда эти два термина выражены полностью совпадающими по объёму (тождественными, равнозначными) именами.
Дата добавления: 2015-09-05; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| V Пример | | | V Пример |