Функции одной переменной

1. Какая функция одной переменной называется дифференцируемой?

Рассмотрим поведение функции в окрестности произвольной точки х₀, приращение аргумента обозначим Dх = х − х₀, а приращение функции обозначим Df = f(x) − f(x₀).

Если в окрестности данной точки приращение функции можно представить в виде суммы линейного члена АDх и ошибки e, порядок малости которой выше первого, то функция называется дифференцируемой в точке x₀, а линейная часть приращения АDх называется первым дифференциалом и обозначается df; при этом коэффициент А называется первой производной в точке x₀

Df = f(x) − f(x₀) = df + e = АDх + o (Dx); т.е.:

df = АDх и e = o (Dx);

При этом по умолчанию полагаем: dх = Dх

2. Что такое первая производная?

Скорость роста функции в точке х₀, − коэффициент при Dх в первом дифференциале. Наглядно: прирост функции при увеличении аргумента на единиц у. Формально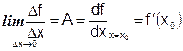

3. Выпуклость функции

Функция называется выпуклой вверх на интервале, если на этом интервале ее график лежит ВЫШЕ любой ее ХОРДЫ (или, что то же самое, лежит НИЖЕ любой ее КАСАТЕЛЬНОЙ).

Функция называется выпуклой вниз на интервале, если на этом интервале ее график лежит НИЖЕ любой ее ХОРДЫ (или, что то же самое, лежит ВЫШЕ любой ее КАСАТЕЛЬНОЙ)

Т.е. выпуклая вниз функция обгоняет свою касательную, а выпуклая вверх функция от нее отстает

4. Второй дифференциал и вторая производная

Если в окрестности данной точки приращение функции можно представить в виде суммы линейного члена АDх квадратичного члена ВDх² и ошибки e, порядок малости которой выше второго − o (Dx²), то функция называется дважды дифференцируемой в точке x₀, линейная часть приращения АDх называется первым дифференциалом и обозначается df, квадратичная часть приращения ВDх² называется вторым дифференциалом и обозначается d²f.

Df = f(x) − f(x₀) = df + d²fe = АDх + BDх² + o (Dx²);

df = АDх

d²f = BDх²

При этом:

- коэффициент А называется первой производной в точке x₀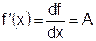

- половина коэффициента В называется второй производной в точке x₀, она равна производной от первой производной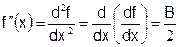

5. Точка перегиба

На том интервале, где 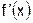< 0 функция выпукла вверх, там, где 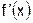> 0 функция выпукла вниз. В точке, где вторая производная равна нулю и при этом меняет знак, происходит смена выпуклости вверх на выпуклость вниз или наоборот.

Такая точка, в которой происходит смена типов выпуклости, называется точкой перегиба, если в точке перегиба у функции есть вторая производная, то она непременно равна нулю.

Дата добавления: 2015-09-05