Вычислить отклик импульсной системы с идеальным квантователем на входе на заданное входное воздействие.

В соответствии с таблицами преобразования Лапласа:

Если 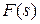изображение по Лапласу непрерывной функции времени ,

то - есть изображение функции .

Итак, умножение функции комплексной переменной 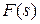на 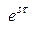соответствует смещению во времени на величину возможного - оригинала функции .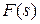

Далее:

умножение функции комплексной переменной на соответствует

сдвигу во времени на величину возможного -оригинала функции .

В таблицах -преобразований имеются -преобразования смещенных

на последовательностей (на 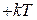-упреждающих и на - запаздывающих).

На рис. ниже показано смещение последовательностей при

влево (упреждение) - f(k+j)

и вправо (запаздывание) - f(k-j):

- преобразование смещенных последовательностей:

1. Упреждение: , (1)

2. Запаздывание: 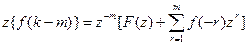, (2)

. (3)

В (3) записано:

·

· - преобразование запаздывающих последовательностей без предыстории: . Умножение -изображений на соответствует сдвигу таких последовательностей на 1 такт в сторону запаздывания.

Импульсную передаточную функцию непрерывной системы с идеальным квантователем на входе находят последовательно вычисляя:

- весовую функцию непрерывной системы

- -изображение весовой функции с заданным интервалом квантования : .

Рассмотрим импульсную, линейную, стационарную систему без упреждения с передаточной функцией: , для таких систем . (4)

!! Порядок системы равен разности наибольшей и наименьшей степеней знаменателя.

Умножим числитель и знаменатель стационарной системы (4) на и перейдем к описанию ее разностным уравнением:

;

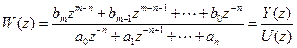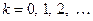(5)

Решение 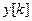разностного уравнения (5) можно найти:

- последовательно вычисляя 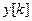для всех 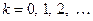, начиная с ,

- используя аппарат z –преобразования, вычисляя 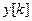в общем виде.

Управление определено при и предыстории не имеет .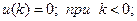

Выполним z –преобразование левой и правой части (5): ;

Здесь полином степени переменной с коэффициентами , например,

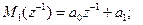
Отсюда, если система до начала действия входного возмущения (до момента времени ) находилась в движении и то:

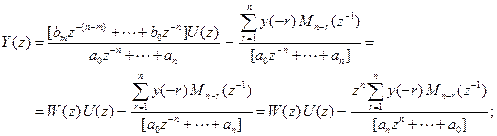
Обратное z-преобразование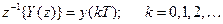

дает выходную последовательность.

- начальные условия для нахождения решения уравнения (5) должны быть известны;

Дата добавления: 2015-08-27