Матричный способ решения

Матричный способ решения СЛАУ (6) достаточно прост. Для начала на Листе1 нужно создать следующую заготовку.

Обе части матричного равенства (2) умножим слева на обратную матрицу А ^-1. Получим A ^-1´ A ´ X = A ^-1´ B. Т.к. A ^-1´ A = E, где E – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы).

Для этого в ячейку В18 введем следующую формулу: = МОБР(В12:Е15)

Нажимаем на «ОК» - появляется первое неизвестное в ячейке В18 (0,13863).

Рис.Диапазон выделенных ячеек В12:Е15

Далее ставим курсор в ячейку В18 (так, чтобы в строке формул видна была наша формула) и выделяем диапазон ячеек В12:Е15. Затем нажимаем клавишу F2 для распространения формулы на ячейки выделенного диапазона

Рис. Распространение формулы на диапазон выделенных ячеек В18:Е21

Далее ставим курсор в строку формул и нажимаем комбинацию клавиш «ctrl+shift+enter» (нужно удерживать вместе ctrl и shift, потом нажать на enter). Появляются восемь оставшихся неизвестных. В итоги мы получили обратную матрицу.

Рис. Получение обратной матрицы в выделенных ячейках В18:Е21

Далее в ячейку I12 введем следующую формулу: =МУМНОЖ(D18:E21;G12:G15)

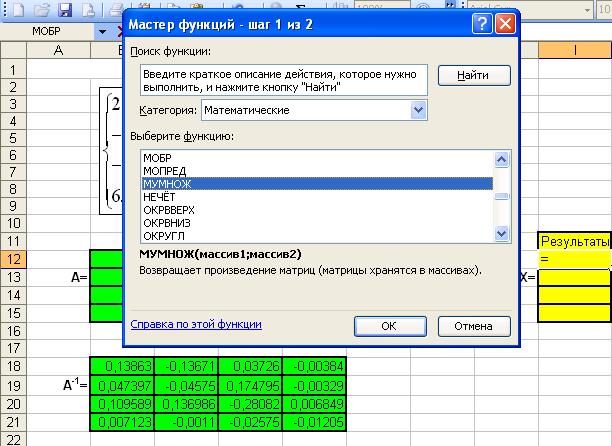
Нажимаем на «ОК» - появляется первое неизвестное в ячейке I12 (-4,3665753).

Далее ставим курсор в ячейку I12 (так, чтобы в строке формул видна была наша формула) и выделяем диапазон ячеек I12:I15. Затем нажимаем клавишу F2 для распространения формулы на ячейки выделенного диапазона

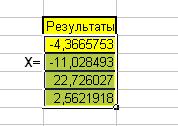
Далее ставим курсор в строку формул и нажимаем комбинацию клавиш «ctrl+shift+enter» (нужно удерживать вместе ctrl и shift, потом нажать на enter). Появляются восемь оставшихся неизвестных. Появляются три оставшихся неизвестных. СЛАУ решена.

Дата добавления: 2015-08-27