Взаимодействие биологических систем.

Математическая теория игр.

Как видим, главной особенностью живых организмов, как управляемых систем, заключается в том, что они могут устойчиво сохранять накопленный в них порядок, только постоянно увеличивая свою популяцию. А это значит, что они обязательно должны вступать в конфликт между собой или между различными популяциями. По сути дела, жизнедеятельность следует рассматривать как постоянный конфликт между различными формами упорядоченных систем.

В настоящее время в кибернетике активно разрабатывается математическая теория игр [18]. Смысл этой теории в том, чтобы понять, кто из двух (трёх, четырёх,...) конфликтующих сторон добьётся выигрыша (применительно к конфликту биологических систем – навяжет свой порядок).

Основными элементами теории игр являются:

Конфликтующие субъекты (игроки, соперники, партнёры) – управляемые системы, каждая из которых стремится навязать природе порядок, отличающийся от порядка соперников.

Природа (окружающая среда, шахматная доска с фигурами, колода карт, рынок и т.п.) – пассивный объект воздействия субъектов игры, меняющий свою конфигурацию (порядок) после каждого хода субъектов или независимо от них.

Ходы игроков и природы – единичные (простейшие) изменения природы под воздействием субъектов игры (личные ходы) или спонтанно в результате произвольного изменения самой природы (случайные ходы).

Правила игры – перечень всех возможных вариантов ходов, а также конечная конфигурация природы, определяемая как победа одной из конфликтующих сторон и поражение другой. В правила включается также процедура выполнения ходов партнёрами: поочерёдная, в зависимости от результатов предыдущего хода, от сложившейся конфигурации природы и т.п.

Ситуация (позиция, вариант) – конфигурация природы, сложившаяся спустя несколько личных и случайных ходов.

Выбор – конкретный ход, который выбирает один из конфликтующих субъектов из всего множества разрешённых для него ходов; исход – конкретный ход, осуществляемый природой.

Лучше всего понять основные количественные соотношения теории игр можно на примере игры[18], включающей в себя двух игроков и природу. Порядок выполнения ходов следующий: 1 игрок – природа – II игрок – природа – 1 игрок – природа... и. т. д. В этом случае игра делится на циклы, каждый из которых состоит из одного хода обоих игроков и двух ходов природы. После каждого 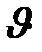- ого цикла у игрока 1 появляется возможность сделать n_1J вариантов ходов, у игрока II – n_2J вариантов. У природы число ходов в два раза больше, зато число возможных вариантов n_n не меняется. Например, если в качестве природы выступает игральная кость, то число возможных вариантов всегда равно шести. В шахматах или шашках ходы природы вообще отсутствуют (число вариантов равно нулю).

Игра заканчивается тогда, когда у кого-то из игроков число возможных вариантов станет равно нулю (т.е. либо n_1Jmax = 0, либо n_2Jmax = 0). Эта ситуация воспринимается как победа противоположной стороны, лишившей данного игрока возможности к дальнейшим действиям (ходам).

Главным понятием игры является стратегия – последовательность выборов одного игрока в ответ на предшествующие ходы соперника и исходы природы от первого до последнего хода. Вариантов таких последовательностей в каждой игре, даже если она относительно проста, чрезвычайно много. Однако ясно, что одна часть множества стратегий приведёт первого игрока к победе, а второго к поражению, а другая – к противоположной ситуации.

Приведём простейший пример: игру в «крестики-нолики» – рисунки 5.2 и 5.3. Как известно, цель каждого игрока – разместить три принадлежащие ему фигуры – крестики игроком I и нолики игроком II – так, чтобы их можно было соединить прямой линией, т.е. либо занять ими три клетки горизонтальной линии, либо три вертикальной, либо три диагональной линии. Чтобы избежать ничьей, иногда к этому условию добавляют ещё одно – в случае, если ни одному из игроков не удаётся выстроить три свои фигуры по прямой линии, выигрывает тот, кто делает последний ход. В этом случае подразделяют «чистый» выигрыш (аналог нокаута в боксе) и выигрыш «по очкам». Нетрудно заключить, что «по очкам» всегда выигрывает (при отсутствии третьего партнёра – природы) игрок I. Это вынуждает игрока II выбирать наиболее агрессивную стратегию.

Ясно, что игрок I, начинающий игру, может сделать девять различных ходов. Игрок II может ответить 8 ходами, так как первая клетка уже занята. В следующий цикл у игрока I остаётся всего семь вариантов ходов. Далее у игрока II остаётся 6 ходов. В следующем цикле у игрока I есть 5 ходов, однако их число фактически меньше, так как при некоторой конфигурации крестиков и ноликов, поставленных в предшествующих циклах, этот игрок выигрывает, поставив три крестика по прямой линии.

На рисунке 5.2, а показаны некоторые варианты выигрыша игрока I на третьем ходу. На самом деле их больше. Другие варианты можно получить из изображённых на рисунке 5.2, а путём симметричного отображения относительно горизонтальной, двух диагональных или вертикальной средней линии. На рисунке возле каждого квадрата показано число симметричных вариантов, соответствующих изображенной на нём конфигурации крестиков и ноликов. Как видим, у игрока I всего 120 стратегий, позволяющих выиграть на третьем ходу (из 9!/4!3!2!=1260 вариантов – множество из девяти клеток подразделяется на три подмножества – крестиков(3 клетки), ноликов (2 клетки) и пустых (4 клетки)).

Согласно §1.6 и [15 ] его статистический вес Р = 9!/4!3!2!. Нетрудно заключить, что 1140 положений на квадрате позволяют игроку II продолжить игру. Третий ход игрока II приводит к 9!/3!3!3! – 120= 1560 вариантам. Часть из них означает его победу. На рисунке 5.2, б так же, как на рисунке 5.2, а, показаны базовые варианты победы игрока II на третьем ходу. Возле каждого квадрата по-прежнему изображаем число симметричных конфигураций, соответствующих представленной на рисунке. Как видим, у игрока II на третьем ходу 140 вариантов выигрыша. Оставшиеся 1560 – 140 = 1420 конфигураций позволяют игроку I продолжить игру, делая четвёртый ход. На рисунке 5.2, в даны базовые конфигурации выигрыша этого игрока на этом ходу и число соответствующих каждой из них симметрий. Как видим, общее число выигранных игроком I на четвёртом ходу позиций равно 256, а оставшихся 9!/4!3!2! – 120 – 140 – 256 = 744. Эти оставшиеся позиции позволяют игроку II сделать четвёртый, последний ход, 96 вариантов которого приносят ему выигрыш – см. рисунок 5.2, г.

У игрока I остаётся ещё 9!/4!4! – 96 –256 – 140 – 120 = 18 позиций, чтобы закончить игру и выиграть партию. (На самом деле у игрока I остаётся всего 9 ходов, так как каждым двум разным позициям соответствует одна свободная клетка). Таким образом, у игрока I всего 120 + 256 + 9 = 385 выигрышных стратегий, а у игрока II – 140 + 96 = 236 стратегий, т.е. в 1,63 раза меньше.

Следует отметить, что все проведённые расчёты исходят из того, что каждый из игроков делает случайные ходы и не «задумывается» об их последствиях – не просчитывает варианты вперёд. Тем не менее, даже в этом случае порядок на доске – в «природе» – увеличивается на

Рисунок 5.2.Варианты выигрыша на третьем ходу игры в крестики – нолики

DI = log₂(385+236) = 9.28 бит,

где величина, стоящая под знаком логарифма – количество всех возможных вариантов до начала игры. Ясно, что стремление «выиграть» ведёт к увеличению степени интеллектуальности игрока, которая определяется способностью выбрать оптимальную стратегию, т.е. как можно лучше просчитать варианты развития событий.

Проанализируем, как можно выбрать оптимальную стратегию игры для игроков I и II. Во-первых, простой анализ показывает, что у игрока I не 9, а только три независимых друг от друга варианта первого хода – рисунок 5.3, а, так как остальные шесть ходов – зеркальные отображения одного из приведённых

Во-вторых, приведённые на рисунке 5.3, а варианты не эквивалентны друг другу: первый (крестик в центре доски) ведёт к четырём выигрышным стратегиям (на рисунке они обозначены стрелками, соединяющими клетки, занятие которых крестиками соответствует «чистой» победе); второй – к двум, третий – к трём. Ясно, что игроку I разумнее всего расположить крестик в центре доски. В ответ на этот ход у игрока II всего два варианта независимых хода – рисунок 5.3, б. Первый обеспечивает две победные стратегии – см. рисунок 5.3, б, а второй – только одну. Ясно, что оптимален для игрока II первый вариант.

Рисунок 5.3

Оптимизация игры в «крестики-нолики»

И действительно, он, в конечном счёте, приводит к победе игрока I «по очкам» - рисунок 5.3, г-м, в то время как второй вариант – к «чистой» победе – рисунок 5., н-у. Стратегии игры можно изобразить графом – рисунок 5.3, в (см. ниже).

Основываясь на этом примере, изложим общие положения теории игр. Множество стратегий игрока I обозначим Х, а игрока II – Y, а их конкретные стратегии – х, у. Кроме этих стратегий существует стратегия случайных ходов природы h. Например, в указанной игре можно добавить ещё одно условие: после поочередного хода обоих игроков подбрасывается монета, и если она выпадает цифрой, то игрок II дополнительно ставит по своему усмотрению крестик (т.е. как бы подыгрывает игроку I). Если монета падает вверх гербом, то, наоборот, игрок I ставит нолик.

Совокупность стратегий h образует третье множество Н. Конкретная партия g представляет совокупность стратегий

g = g{x, y, h}.

Результат этой партии можно обозначить числом L, равным 1, если выигрывает игрок I, или 0, если выигрывает игрок II. Ясно, что L есть функция стратегий x, y, h:

L = L (x, y, h ).

Она называется [15] функцией потерь. Учитывая, что стратегия h – случайная, можно определить её вероятность р(h). Например, при подбрасывании монеты р(h) = 0.5.

Тогда можно определить среднее значение потерь:

L(x,y)= ΣL(x,y,h)p(h);h Î H. (5.2)

В этом случае L(x,y) принимает любые значения от 0 до 1. Таким образом, математически игра G определяется тройкой множеств

G = {X, Y, L}, (5.3)

где Х, Y – некоторые множества, а L – числовая функция, определённая на произведении Х´Y. Элементы множеств х_i Î X, y_j Î Y называются стратегиями игроков I и II, а функция L – функцией потерь. Числа m и n определяют число стратегий первого и второго игроков.

Цель игры для первого игрока – максимизировать L, а второго – её минимизировать. Всего значений L – m´n и они образуют матрицу:

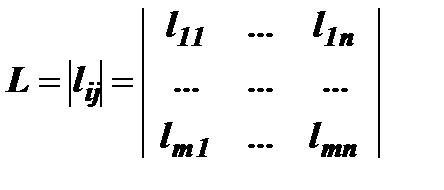. (5.4)

Особую роль играют так называемые статистические игры. Они отличаются от предыдущих – стратегических игр – тем, что в них всего один игрок и природа. Игрок в статистических играх именуется статистиком. Ясно, что в этих играх функция потерь зависит от всевозможных состояний природы h и стратегий статистика х:

L = L (x, h). (5.5)

Для того чтобы представить себе взаимодействие стратегий в процессе игры, обычно прибегают к древовидному графу. На рисунке 5.3, в построен граф игры в крестики-нолики, описанной выше без «статистического» игрока.

Как видим, игры, независимо от того, где они происходят, носят очевидный антиэнтропийный характер: победу в них в подавляющем большинстве случаев одерживает тот партнёр, у которого степень упорядоченности (точнее степень устойчивости упорядоченности) выше. Результаты игры приводят к повышению меры упорядоченности в природе (следует не забывать, что под «природой» в теории игр понимается статистический партнёр, т.е. партнёр, действия которого носят случайный, сумбурный характер).

Напомним, что конфликтные ситуации («игры») возникли на Земле в результате появления биологических систем.

Дата добавления: 2015-08-27