Амплитуда и фаза

Метод комплексных амплитуд

Править

Метод расчёта линейных в установившемся режиме в отношении гармонических сигналов.

Этот метод использует обобщения понятий сопротивления, напряжения, силы тока (и прочих) до комплексных величин, являющихся функцией частоты.

Геометрическая интерпретация

Амплитуда и фаза

Гармоническую функцию 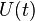можно выразить формулой:

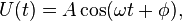
где

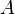§ — амплитуда,

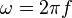§ — циклическая частота,

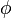§ — начальная фаза.

Для электрических систем функция 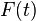может описывать напряжение (приведено для примера), силу тока, магнитный поток, заряд, а также в приложении к электрическим средам — проекции электрического поля, плотности тока и т. п.

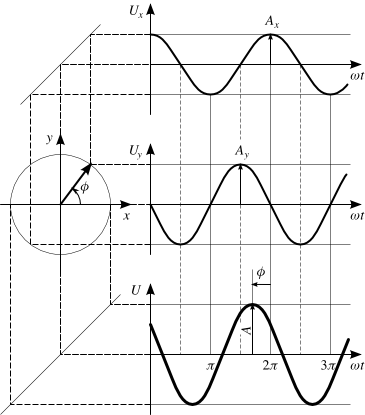
Эти два параметра можно представить в виде вектора на плоскости, где амплитуда — длина, а фаза — угол, отсчитанный по традиции от положительного направления оси абсцисс против часовой стрелки.

Изменение сигнала по времени можно представить вращением вектора вокруг начала координат против часовой стрелки с угловой скоростью ω, и тогда проекция вектора на ось x или у будет описывать гармоническую функцию:

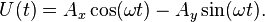
Дата добавления: 2015-08-27