
|
Читайте также: |
Характерной особенностью современного состояния радиотехники и радиофизики является все более широкое использование статистических методов. Многие явления, для изучения которых казалось вполне достаточным применение классических методов математической физики, при более глубоком изучении потребовали вероятностного подхода. Статистическая природа многих физических объектов, непредсказуемый, случайный характер шумов и помех, сопутствующих работе всех радиофизических устройств, привели к тому, что статистические методы проникли буквально во все разделы радиофизики и радиотехники.
Статистическая радиофизика представляет собой в настоящее время широкую и быстро развивающуюся область, включающую в себя как чисто физические проблемы, так и разнообразные прикладные вопросы. Важную теоретическую и практическую задачу представляет собой статистический анализ быстро протекающих и резко изменяющихся процессов и явлений, при которых зависимости тех или иных физических величин от времени имеют импульсный характер. Причем параметры импульсов, как правило, неизвестны или известны неточно, а их наблюдение и регистрация сопровождаются различными флуктуационными явлениями и шумами.
Статистический анализ импульсных сигналов с неизвестными параметрами находит широкое применение в связи и локации с использованием электромагнитных, акустических и других типов волн, при радиофизических исследованиях различных сред и объектов, в теории и технике радиоуправления, телеметрии, навигации, промышленной диагностике и др. При этом во многих приложениях [1] в качестве модели импульсного процесса используется прямоугольный видео или радиоимпульс. Дальнейшим обобщением этой модели является класс сигналов со случайной субструктурой, представляющих собой результат амплитудной модуляции прямоугольного импульса реализацией стационарного гауссовского случайного процесса, время корреляции которого значительно меньше длительности импульса. Примерами таких сигналов могут служить информационный сигнал в системах связи с шумовой несущей [2], сигнал, искаженный модулирующей помехой [3], импульс, описывающий вспышку оптического шума [4], взрывного шума в транзисторах и др. Если форма импульса достаточно сложная и априори неизвестна, то для его описания можно также использовать реализации случайного процесса [4].
Среди задач статистического анализа импульсов со случайной субструктурой на первый план выступают вопросы обнаружения импульсов и оценивания их неизвестных параметров. Одним из наиболее распространенных на практике методов анализа импульсных процессов являются методы, основанные на их временной фиксации. Однако при наличии у импульсов случайной субструктуры и при увеличении мощности ее флуктуационной составляющей такие методы становятся далекими от оптимальных. Указанные задачи предпочтительнее решать с помощью методов теории статистических решений [5-7 и др.], оптимальных в том или ином смысле. В случае если имеется полное статистическое описание наблюдаемых данных и заданы потери при принятии всех возможных решений, то можно построить строго оптимальные байесовские правила обнаружения и оценивания. Однако, на практике эти условия, как правило, не выполняются. Нередко неизвестны априорные вероятности наличия или отсутствия импульса в наблюдаемых данных, априорные распределения неизвестных параметров импульса, возникают трудности задания потерь при принятии тех или иных решений. Поэтому особенно широкое распространение получил метод максимального правдоподобия (МП) [5-7 и др.], требующий меньшего объема априорной информации и являющийся асимптотически оптимальным для широкого класса сигналов, функций распределения и потерь. Использование этого метода для анализа импульсов со случайной субструктурой позволяет синтезировать более простые, чем при использовании байесовского подхода, но достаточно эффективные алгоритмы обработки.
Цель дипломной работы состоит в исследовании алгоритмов оценки параметров случайной субструктуры прямоугольного импульса при наличии мультипликативной и аддитивной помех и ошибок синхронизации.
1 ПРИЕМ случайных импульсных сигналов ПРИ НАЛИЧИИ ПОГРЕШНОСТЕЙ ТАКТОВОЙ СИНХРОНИЗАЦИИ
1.1 Постановка задачи
Пусть на интервале времени  наблюдается аддитивная смесь полезного сигнала
наблюдается аддитивная смесь полезного сигнала 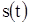 и шума
и шума  :
:
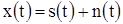 . (1.1)
. (1.1)
Полезный сигнал 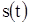 представляет собой гаусовский импульсный
представляет собой гаусовский импульсный  стохастический сигнал, который можно представить как случайную функцию вида
стохастический сигнал, который можно представить как случайную функцию вида
 ,
,  (1.2)
(1.2)
где  – время прихода,
– время прихода,  – длительность импульса, а
– длительность импульса, а 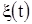 – широкополосный стационарный случайный процесс с математическим ожиданием (МО)
– широкополосный стационарный случайный процесс с математическим ожиданием (МО)  и спектральной плотностью (СП)
и спектральной плотностью (СП)
 (1.3)
(1.3)
(функцией корреляции  ). Здесь
). Здесь  – ширина полосы частот, а
– ширина полосы частот, а  – дисперсия процесса
– дисперсия процесса 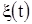 .
.
Импульсный сигнал (1.2) можно рассматривать как результат амплитудной модуляции прямоугольного видеоимпульса реализацией гаусовского случайного процесса 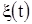 . Примерами таких сигналов могут служить импульсы со случайной субструктурой описывающие вспышку оптического шума, информационный сигнал в системах связи шумовой несущей, сигнал искаженный модулирующей помехой и др.
. Примерами таких сигналов могут служить импульсы со случайной субструктурой описывающие вспышку оптического шума, информационный сигнал в системах связи шумовой несущей, сигнал искаженный модулирующей помехой и др.
Помеху  аппроксимируем гауссовским белым шумом с математическим ожиданием (МО)
аппроксимируем гауссовским белым шумом с математическим ожиданием (МО) 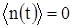 и односторонней спектральной плотностью
и односторонней спектральной плотностью 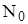 .
.
По наблюдаемой реализации  необходимо оценить (измерить) МО
необходимо оценить (измерить) МО 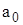 случайного импульсного сигнала
случайного импульсного сигнала 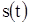 . При этом временное положение
. При этом временное положение  импульса также может быть неизвестно и принимать значения из априорного интервала
импульса также может быть неизвестно и принимать значения из априорного интервала  .
.
1.2 Оценка математического ожидания импульсного сигнала при отсутствии ошибок синхронизации
При синтезе алгоритма оценки воспользуемся методом максимального правдоподобия (МП) [1-5]. Согласно этому методу необходимо формировать логарифм функционала отношения правдоподобия (ЛФОП)  как функцию неизвестной амплитуды. На основании результатов работ [1-3] выражение для ЛФОП можно представить в виде
как функцию неизвестной амплитуды. На основании результатов работ [1-3] выражение для ЛФОП можно представить в виде
 (1.4)
(1.4)
где  – отклик фильтра с импульсной характеристикой
– отклик фильтра с импульсной характеристикой  на реализацию наблюдаемых данных
на реализацию наблюдаемых данных 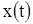 (1.1), причем передаточная функция
(1.1), причем передаточная функция  этого фильтра удовлетворяет условию
этого фильтра удовлетворяет условию  ,
,  ,
,  .
.
Оценка максимального правдоподобия (ОМП) неизвестной амплитуды 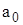 определяется как положение наибольшего максимума ЛФОП по переменной а:
определяется как положение наибольшего максимума ЛФОП по переменной а:
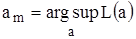 . (1.5)
. (1.5)
Положение наибольшего максимума ЛФОП  является решением системы уравнения и неравенства:
является решением системы уравнения и неравенства:


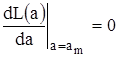 ,
, 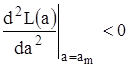 . (1.6)
. (1.6)
Согласно (1.3)
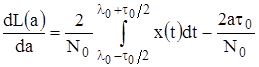 . (1.7)
. (1.7)
Тогда ОМП 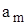 параметра
параметра 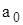 запишется в виде
запишется в виде
 .
.  (1.8)
(1.8)
Алгоритм (1.8) можно реализовать с помощью измерителя, структурная схема которого показана на рисунке.

Рисунок Максимально-правдоподобный измеритель математического ожидания случайного импульсного сигнала
Здесь обозначено: 1 – ключ открывающийся на время 
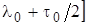 , 2 – интегратор, 3 – делитель.
, 2 – интегратор, 3 – делитель.
Рассмотрим характеристики оценки 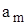 (1.8). Поскольку аддитивная помеха
(1.8). Поскольку аддитивная помеха  является гауссовской, то ОМП (1.8) является гауссовской случайной величиной. Поэтому ее эффективность полностью (в статистическом смысле) характеризуется условными смещением
является гауссовской, то ОМП (1.8) является гауссовской случайной величиной. Поэтому ее эффективность полностью (в статистическом смысле) характеризуется условными смещением  , дисперсией
, дисперсией  и связанным с ними рассеянием
и связанным с ними рассеянием  .
.
Согласно определению условное смещение ОМП 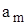 (1.8) найдем путем ее непосредственного усреднения по реализациям
(1.8) найдем путем ее непосредственного усреднения по реализациям  :
:
 . (1.9)
. (1.9)
Подставляя формулы (1.1), (1.2) в (1.9) и учитывая, что 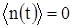 , получаем:
, получаем:
 . (1.10)
. (1.10)
Таким образом, ОМП (1.8) при априори известных остальных параметрах импульса является условно (а, следовательно, и безусловно) несмещенной.
Аналогично можно найти условную дисперсию ОМП (1.9):

(1.11)
Подставляя (1.1), (1.2) в (1.11), получаем:
 (1.12)
(1.12)
Поскольку сигнал и шум статически независимы, то  . Кроме того,
. Кроме того, 
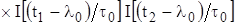 ,
, 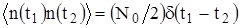 , где
, где  – корреляционная функция процесса
– корреляционная функция процесса 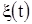 , а
, а  – дельта-функция. С учетом трех последних равенств из (1.12) получаем
– дельта-функция. С учетом трех последних равенств из (1.12) получаем
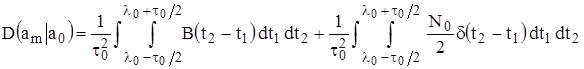 .
.
(1.13)
Для вычисления первого интеграла в (1.13) сделаем замену переменных:  ,
,  . Тогда, полагая, что флуктуации процесса
. Тогда, полагая, что флуктуации процесса 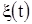 являются «быстрыми», т.е. выполняется условие
являются «быстрыми», т.е. выполняется условие  , имеем:
, имеем:
 (1.14)
(1.14)
Для вычисления второго интеграла в (1.13) используем фильтрующее свойство δ-функции:  . Тогда находим:
. Тогда находим:
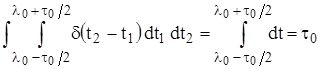 (1.15)
(1.15)
Подставляя (1.14), (1.15) в (1.13) для дисперсии оценки 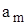 окончательно получаем
окончательно получаем
 (1.16)
(1.16)
Поскольку ОМП (1.8) является несмещенной, то дисперсия оценки 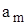 совпадает с ее рассеянием:
совпадает с ее рассеянием:
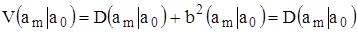 . (1.17)
. (1.17)
Из формул (1.10), (1.16), (1.17) следует, что точность ОМП (1.8) МО случайного импульсного сигнала (1.2) не зависит от искаженного значения параметра 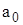 . Дисперсия оценки МО, с одной стороны, возрастает с увеличением спектральной плотности
. Дисперсия оценки МО, с одной стороны, возрастает с увеличением спектральной плотности  и N0 процесса
и N0 процесса 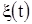 и шума
и шума  , а, с другой стороны, уменьшается с увеличением длительности измеряемого импульса. Выражения (1.10), (1.16), (1.17) позволяют сделать обоснованный выбор длительности полезного сигнала в зависимости от требуемой эффективности МП измерителя и уровня аддитивных помех.
, а, с другой стороны, уменьшается с увеличением длительности измеряемого импульса. Выражения (1.10), (1.16), (1.17) позволяют сделать обоснованный выбор длительности полезного сигнала в зависимости от требуемой эффективности МП измерителя и уровня аддитивных помех.
1.3 Оценка амплитуды импульсного сигнала при наличии погрешностей синхронизации
Предположим теперь, что временное положение  импульса (1.2) неизвестно, но имеется независимый от наблюдаемой реализации (1.1) канал синхронизации, формирующий опорный синхроимпульс с временным положением
импульса (1.2) неизвестно, но имеется независимый от наблюдаемой реализации (1.1) канал синхронизации, формирующий опорный синхроимпульс с временным положением  , в общем случае не равным
, в общем случае не равным  . Обозначим через
. Обозначим через 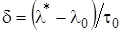 относительную погрешность синхронизации. Используя при синтезе алгоритма оценивания по методу МП вместо неизвестного параметра
относительную погрешность синхронизации. Используя при синтезе алгоритма оценивания по методу МП вместо неизвестного параметра  его прогнозируемое (ожидаемое) значение
его прогнозируемое (ожидаемое) значение  , получим оценку:
, получим оценку:
 , (1.18)
, (1.18)
которую, в отличие от ОМП (1.8), назовем квазиправдоподобной оценкой (КПО). При КПО  (1.18) переходит в ОМП
(1.18) переходит в ОМП 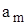 (1.8)
(1.8)
Найдем характеристики оценки 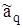 . Аналогично (1.9) смещение КПО (1.18) запишется в виде:
. Аналогично (1.9) смещение КПО (1.18) запишется в виде:
 . (1.19)
. (1.19)
Подставляя (1.1), (1.2) в (1.19) и учитывая, что 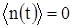 , получаем:
, получаем:
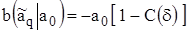 ,
,  (1.20)
(1.20)
Из формулы (1.20) и следует, что наличие погрешностей синхронизации приводит к появлению отрицательного смещения оценки амплитуды, которое возрастает с увеличением относительной погрешности синхронизации δ. Такое поведение смещения оценки обусловлено несовпадением интервала 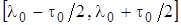 локализации сигнала на оси времени и интервала интегрирования
локализации сигнала на оси времени и интервала интегрирования  при вычислении КПО (1.18).
при вычислении КПО (1.18).
Аналогично (1.11) найдем дисперсию оценки 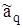 :
:
 .
.
(1.21)
Подставляя (1.1), (1.2) в (1.21), находим:
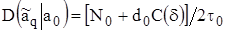 , (1.22)
, (1.22)
Соответственно рассеяние КПО 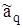 определяется как
определяется как
 . (1.23)
. (1.23)
Из (1.23) следует, что с ростом погрешности синхронизации δ рассеяние КПО (1.18) монотонно возрастает, и, следовательно, точность оценки МО случайного импульсного сигнала ухудшается. Ухудшение точности оценки обусловлено как появлением смещения, так и зависимостью дисперсии оценки (1.18) от ошибок синхронизации. Формулы (1.20), (1.22), (1.23) позволяют оценить качество квазиправдоподобного алгоритма оценки (1.18) в каждом конкретном случае.
Дата добавления: 2015-08-27; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ | | | ОРГАНИЗАЦИОННО-ЭКОНОМИЧЕСКАЯ ЧАСТЬ |