Теория принятия решений

Изучением того, как человек принимает решения, и созданием методов выбора занимаются многие научные дисциплины, которые возникли и исторически развивались независимо друг от друга. К ним относятся теория принятия решений, системный анализ, исследование операций, теория статистических решений, теория игр, теория оптимального управления, экономическая кибернетика, теория организаций, информатика, искусственный интеллект, когнитивная психология, теория поведения и др. Эти дисциплины с разных точек зрения анализируют механизмы, процессы и правила выбора применительно к объектам различной природы и в различных условиях их существования. Все вместе они образуют многодисциплинарную науку, помогающую человеку сделать обоснованный выбор. Теория принятия решений как самостоятельное научное направление стала складываться в середине ХХ в. в рамках методологии системного анализа, хотя самые первые работы по исследованию голосования как способа коллективного выбора появились еще в конце XVII в. Основное назначение теории принятия решений состоит в разработке методов и средств, позволяющих одному человеку или группе лиц сформулировать множество возможных вариантов решения проблемы, сравнить их между собой, найти среди них лучшие или допустимые варианты, которые удовлетворяют тем или иным требованиям (ограничениям), и при необходимости объяснить сделанный выбор.

Теория принятия решений может оказать существенную помощь в анализе и решении сложных проблем, но лишь тогда, когда ее методологические и математические средства применяются «правильно», соответственно их возможностям, не преувеличивая и не умаляя их роли в процессе нахождения решения. Поэтому теорию принятия решений правильнее было бы назвать теорией поиска и обоснованного выбора наиболее предпочтительных для человека вариантов решения проблемы.

Существуют две противоположные точки зрения на роль формальных методов при решении практических проблем выбора. Люди, профессионально не владеющие математическими методами, нередко считают, что любая проблема может быть формально переведена на язык математики и потом решена ее средствами. Другие полностью отвергают такие возможности. Действительность же гораздо сложнее этих крайних утверждений.

Любые ситуации, требующие принятия решения, содержат, как правило, большое число неопределенных факторов, которые оказывают влияние как на формальную постановку задачи, так и на средства ее решения. Эти неопределенные факторы можно в самом общем виде разбить на три группы.

Прежде всего это так называемая неопределенность природы, т.е. факторы людям попросту неизвестные или от них не зависящие. Затем - неопределенность человека, который может вести себя непоследовательно, противоречиво, допускать ошибки, зависеть от других лиц (партнеров, противников и т.д.), чьи действия он не может полностью учесть или предвидеть. И наконец, неопределенность целей, которые могут различаться и не совпадать друг с другом. Например, авиаконструкторы, проектируя самолет, должны учитывать его целевое назначение, заданные показатели скорости, грузоподъемности и дальности полета, условия безопасности и комфортности для экипажа и пассажиров, факторы экономичности и технологичности производства и эксплуатации самолета, экологические требования и многие другие обстоятельства.

Ясно, что полностью свести подобные задачи с неопределенностью к корректно поставленным математическим задачам нельзя в принципе. Чтобы сделать возможным их решение, надо как-то ограничить, уменьшить или, как говорят, «снять» неопределенность. Для этого проводится содержательный анализ проблемной ситуации, делаются какие-либо предположения и вводятся упрощения в постановку задачи. И именно средства, входящие в состав тех или иных методов принятия решений, очень часто позволяют получить дополнительную информацию, нужную для формализации реальной проблемной ситуации и приведения ее к виду, пригодному для использования математически методов и получения приемлемого результата.

Говоря о практической применимости методов принятия решений, следует особенно подчеркнуть, что должны существовать как объективные внешние обстоятельства, таки субъективные внутренние условия, которые побуждали бы человека - руководителя, ответственного за решение стоящей проблемы, специалиста, аналитика – искать лучшие варианты ее решения. Без такой потребности спрос на научно обоснованные методы выбора будет невелик.

Анализ системы автоматизированного поиска по таблицам

Имеется прямоугольная таблица. Столбцам соответствуют некоторые параметры, строкам соответствуют некоторые действия. Строки могут быть сгруппированы, при этом, группировка указывается в крайних слева столбцах таблицы. Группировки в крайних столбцах могут не совпадать.

Примерный вид таблицы.

Способ покрытия	Вид покрытия	Материал трущейся пары	Размеры	Пар 1	Пар I	Пар N
Напыление	Баббит	Бронза + бронза	Диаметр 50мм	14, 0.04
Силумин	Диаметр 100мм
Электролиз	Диаметр 150мм
Напыление	Бронза + сталь
Наваривание	Баббит	Сталь + сталь
Хром
Латунь + бронза
Электролиз	Латунь + латунь

За пример взят фрагмент технологической таблицы трущейся пары (шарнир), заполнение приблизительное. Число параметров может быт в пределах до 2х сотен. Число строк в принципе не ограничено, но обычно не более сотни (это для механики, но в других предметных областях может быть больше). Число столбцов группировок не более 10.

Ведущая группировка здесь материал трущейся пары, остальные вспомогательные. В ведущей группировке повторов нет, во вспомогательных возможны. Вещая группировка в таблице всегда одна, но должен быть механизм замены ведущей группировки и соответствующей перестройки таблицы.

Ячейки таблицы заполняют значения параметров с их допусками, например, 14±0.04 (можно просто пару (14, 0.04)).

Таблицы используются для поиска и принятия решений. Для этого назначается ряд критериальных параметров (т.е. столбцов, значения параметров которых будет оцениваться). Задаются значения критериальных переменных для поиска требуемой строки или набора строк. Критериальные переменные в каждой строке оцениваются по специальной функции с учетом заданных значений поиска, и сводятся в интегральный показатель строки. Далее интегральные показатели строк сравниваются и выбирается строка или набор строк для которых значение интегрального показателя оказалось наилучшим. Для сужения поиска могут быть также заданы отдельные группировки (например, в приведенном фрагменте – диаметры), тогда строки не входящие в заданные группировки игнорируются.

Подбор оценочной функции системы автоматизированного поиска по таблицам.

Оценочную функцию подбираем таким образом, чтобы в области допустимых значений переменной, принадлежали бы интервалу [0,1], была безразмерной, определялась бы однозначно и была бы линейной или хотя бы кусочно-линейной.

Функция оценки значения переменной для некоторого шага моделирования или момента актуализации информации t принимается равной:

ì (x_i¢¢-x_i)/(x_i¢¢- x_i¢), если x_i < x_i¢;

ï ((x_i°-s_i)-x_i)/((x_i°-s_i)-x_i¢), если x_i¢£ x_i< x_i°-s_i;

y(x_i)=í 0, если x_i°-s_i £ x_i £ x_i°+s_i;

ï (x_i-(x_i°+s_i))/(x_i¢¢-(x_i°+s_i)), если x_i°+s_i<x_i£ x_i¢¢;

î (x_i-x_i¢)/(x_i¢¢- x_i¢), если x_i> x_i¢¢.

Где:

x_i - значение параметра в ячейке

x_i¢ - нижняя граница заданных для поиска значений,

x_i¢¢ - верхняя граница заданных значений,

x_i° - предпочтительное (оптимальное) значение,

s_i - допускаемое отклонение значений заданного значения от предпочтительного, при котором значение продолжает считаться оптимальным (x_iÎ[x_i°-s_i, x_i°+s_i]).

Функцию является кусочно-линейной, y(x_i)=ax_i+b, где значения a и b будут меняться в зависимости от участка области изменения функции. Чем меньше значение функции, тем ближе к оптимуму (в оптимальной окрестности оно равно нулю).

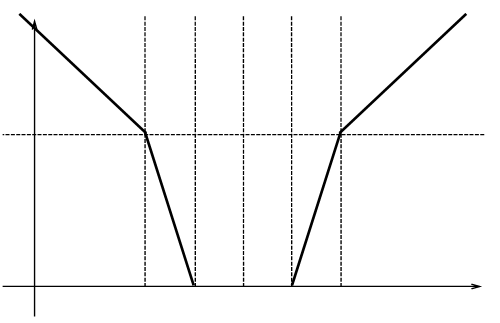
Функция принимает значение только в области положительных чисел, так как выражения вычисляющие значения функции в каждом интервале ее значений составлены так, что всегда меньшее вычитается из большего, имеет два интервала монотонности. Функция показывает относительное приближение значения переменной к некоторому базовому интервалу. Вне промежутка допустимых значений скорость изменения функции меньше, чем внутри области допустимых значений

Вид графика функции y(x_i) приведен ниже.

Все критериальные переменные в строке оцениваются при помощи данной функции

Интегральная оценка строки Y_j=max(y(x_i)), где j – индекс строки.

i

Выбирается строка или набор строк (что вряд ли), для которой значения критерия

Y=max(Y_j). Все критериальные переменные считаются одинаковой важности.

J

Для всех параметров производятся расчеты для значений плюс допуск и минус допуск, учитывается то значение, для которого значение y(x_i) больше.

Если для какого-либо параметра не предусмотрено оптимальной окрестности, то оптимальной считается одна из границ заданного промежутка значений. Нижняя, если нужно уменьшить, верхняя, если увеличить.

А также рассмотрим некоторые свойства разрабатываемой системы:

· Если вводить приоритетность критериальных переменных, то чем меньше вес, тем приоритетнее переменная, веса в пределах [0,1] (чем вес ближе к нулю, тем переменная важнее, но это не обязательно, так для сведения).

· Полученная строка распечатывается полностью со всеми группировками и параметрами.

· В начале обработки запроса всегда проверяется, есть ли среди сохраненных запросов запрос с аналогичным заданием, тогда искать не надо, выводится ранее полученный результат. Если таблица была изменена, то использовать старые запросы можно только как справочные, даже если параметры запросов совпадают нужно проводить новый поиск.

Выбор и анализ языка программирования для проектирования системы автоматизированного поиска по таблицам.

Выбранным языком программирования стал С++ как изучаемый язык программирования в процессе обучения на специальности 230400.62 «Информационные системы и технологии»

C++ — компилируемый статически типизированный язык программирования общего назначения.

Поддерживает такие парадигмы программирования как процедурное программирование, объектно-ориентированное программирование, обобщённое программирование, обеспечивает модульность, раздельную компиляцию, обработку исключений, абстракцию данных, объявление типов (классов) объектов, виртуальные функции. Стандартная библиотека включает, в том числе, общеупотребительные контейнеры и алгоритмы. C++ сочетает свойства как высокоуровневых, так и низкоуровневых языков. В сравнении с его предшественником — языком C, — наибольшее внимание уделено поддержке объектно-ориентированного и обобщённого программирования.

C++ широко используется для разработки программного обеспечения, являясь одним из самых популярных языков программирования. Область его применения включает создание операционных систем, разнообразных прикладных программ, драйверов устройств, приложений для встраиваемых систем, высокопроизводительных серверов, а также развлекательных приложений (игр). Существует множество реализаций языка C++, как бесплатных, так и коммерческих и для различных платформ. Например, на платформе x86 это GCC, Visual C++, Intel C++ Compiler, Embarcadero (Borland) C++ Builder и другие. C++ оказал огромное влияние на другие языки программирования, в первую очередь на Java и C#.

Синтаксис C++ унаследован от языка C. Одним из принципов разработки было сохранение совместимости с C. Тем не менее, C++ не является в строгом смысле надмножеством C; множество программ, которые могут одинаково успешно транслироваться как компиляторами C, так и компиляторами C++, довольно велико, но не включает все возможные программы на C.

Язык возник в начале 1980-х годов, когда сотрудник фирмы Bell Labs Бьёрн Страуструп придумал ряд усовершенствований к языку C под собственные нужды. [4] Когда в конце 1970-х годов Страуструп начал работать в Bell Labs над задачами теории очередей (в приложении к моделированию телефонных вызовов), он обнаружил, что попытки применения существующих в то время языков моделирования оказываются неэффективными, а применение высокоэффективных машинных языков слишком сложно из-за их ограниченной выразительности. Так, язык Симула имеет такие возможности, которые были бы очень полезны для разработки большого программного обеспечения, но работает слишком медленно, а язык BCPL достаточно быстр, но слишком близок к языкам низкого уровня и не подходит для разработки большого программного обеспечения.

Вспомнив опыт своей диссертации, Страуструп решил дополнить язык C (преемник BCPL) возможностями, имеющимися в языке Симула. Язык C, будучи базовым языком системы UNIX, на которой работали компьютеры Bell, является быстрым, многофункциональным и переносимым. Страуструп добавил к нему возможность работы с классами и объектами. В результате практические задачи моделирования оказались доступными для решения как с точки зрения времени разработки (благодаря использованию Симула-подобных классов), так и с точки зрения времени вычислений (благодаря быстродействию C). В первую очередь в C были добавлены классы (с инкапсуляцией), наследование классов, строгая проверка типов, inline-функции и аргументы по умолчанию. Ранние версии языка, первоначально именовавшегося «C with classes» («Си с классами»), стали доступны с 1980 года.

Разрабатывая C с классами, Страуструп написал программу cfront[en] — транслятор, перерабатывающий исходный код C с классами в исходный код простого C. Это позволило работать над новым языком и использовать его на практике, применяя уже имеющуюся в UNIX инфраструктуру для разработки на C. Новый язык, неожиданно для автора, приобрёл большую популярность среди коллег и вскоре Страуструп уже не мог лично поддерживать его, отвечая на тысячи вопросов.

К 1983 году в язык были добавлены новые возможности, такие как виртуальные функции, перегрузка функций и операторов, ссылки, константы, пользовательский контроль над управлением свободной памятью, улучшенная проверка типов и новый стиль комментариев (//). Получившийся язык уже перестал быть просто дополненной версией классического C и был переименован из C с классами в «C++». Его первый коммерческий выпуск состоялся в октябре 1985 года.

До начала официальной стандартизации язык развивался в основном силами Страуструпа в ответ на запросы программистского сообщества. Функцию стандартных описаний языка выполняли написанные Страуструпом печатные работы по C++ (описание языка, справочное руководство и так далее). Лишь в 1998 году был ратифицирован международный стандарт языка C++: ISO/IEC 14882:1998 «Standard for the C++ Programming Language»; после принятия технических исправлений к стандарту в 2003 году — следующая версия этого стандарта — ISO/IEC 14882:2003.

Дата добавления: 2015-08-27