Матрицы. Действия над ними. Обратная матрица.

Произведением матрицы размеров 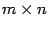на матрицу 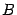размеров называется матрица размеров , элементы которой вычисляются по формуле

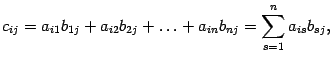
(14.5)

где , .

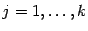Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой -- второй.

Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.

В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.

Правило вычисления элементов произведения можно сформулировать следующим образом.

Для того, чтобы вычислить элемент произведения, стоящий в 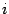-ой строке и -ом столбце, нужно взять 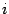-ую строку первого сомножителя и -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).)

Пример Даны матрицы , 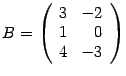. Найдите произведения 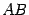и .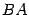

Решение. Рассмотрим произведение 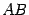. Число столбцов в первом сомножителе равно 3, число строк во втором сомножителе 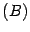тоже равно 3. Числа совпали, следовательно, произведение определено.

Результатом умножения будет матрица , , у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица имеет размеры .

Находим элемент . В его вычислении участвует первая строка первого сомножителя и первый столбец второго сомножителя :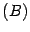

Находим элемент . В его вычислении участвует первая строка первого сомножителя и второй столбец 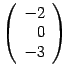второго сомножителя :

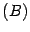Все элементы первой строки матрицы вычислены. Находим элемент . В его вычислении участвует вторая строка первого сомножителя и первый столбец второго сомножителя :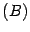

Находим элемент 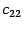. В его вычислении участвует вторая строка первого сомножителя и второй столбец 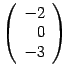второго сомножителя :

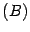Вычислены все элементы второй строки матрицы . Аналогично находим элементы третьей строки:

Итак, .

Рассмотрим произведение 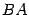. Число столбцов в первом сомножителе 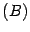равно 2, число строк во втором сомножителе равно 3. Числа не совпали, следовательно, произведение не определено.

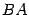Ответ: , произведение не определено.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

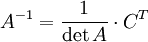
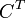— транспонированная матрица алгебраических дополнений;

Полученная матрица A ⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

Транспонированная матрица — матрица , полученная из исходной матрицы 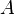заменой строк на столбцы.

Дата добавления: 2015-08-27