Синусоидальные величины и их символическое изображение

Мгновенные значения синусоидальной величины определяются выражением:

,

где – амплитуда;

– действующее значение;

– угловая частота, [с^-1];

– линейная частота, [Гц];

– период колебаний [c];

y – начальная фаза, [рад].

Расчет цепей переменного тока облегчается, если изображать гармонические токи, напряжения и ЭДС векторами на комплексной плоскости.

Совокупность векторов, изображающих синусоидальные функции в заданный момент времени, называется векторной диаграммой.

Комплексное число может быть представлено в алгебраической и показательной форме:

.

Переход из показательной формы в алгебраическую форму осуществляется по формуле Эйлера:

.

При обратном переходе: 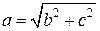, если вещественная часть алгебраической формы положительная, то а если вещественная часть отрицательная, то

.

Комплексная синусоидальная функция представляется в виде вращающегося вектора на комплексной плоскости:

;

,

,

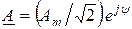(при t = 0).

Мгновенное значение синусоидальной функции есть проекция вращающегося вектора на мнимую ось:

.

Обозначения:

i, u, e – мгновенные значения тока, напряжения, ЭДС.

I _m, U _m, E _m – комплексные амплитудные значения тока, напряжения, ЭДС.

I, U, E – комплексные действующие значения тока, напряжения, ЭДС.

Дата добавления: 2015-08-27