
Читайте также:
|
| dч,мкм | <10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-86 | 86-100 | >100 |

| 0,08 | 0,09 | 0,08 | 0,07 | 0,06 | 0,05 | 0,12 | 0,05 | 0,4 |
| Д | 0,08 | 0,17 | 0,25 | 0,32 | 0,38 | 0,43 | 0,55 | 0,60 | ____ |
| X | -1,4 | -0,95 | -0,67 | -0.46 | -0,3 | -0,17 | 0.13 | 0.26 | ____ |
| dгр | ____ | ||||||||
| Lg dч | 1,0 | 1,301 | 1,477 | 1,602 | 1,699 | 1,778 | 1,934 | 2,0 | ____ |
Данные дисперсного анализа хорошо описываются уравнением прямой  в вероятностно - логарифмической системе координат (Х,
в вероятностно - логарифмической системе координат (Х,  ). Это соответствует логарифмически – нормальному закону распределения частиц по размерам.
). Это соответствует логарифмически – нормальному закону распределения частиц по размерам.
Используя метод наименьших квадратов (МНК) найдем параметры прямой. Для этого необходимо найти минимум функционала:


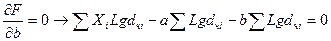
Рассчитаем следующие суммы и подставим их в полученную систему из двух уравнений:
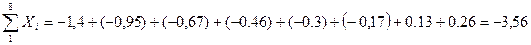








Решение системы:

 ;
; 

 .
.
 ;
;  0
0
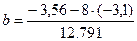 .
. 
Медианный размер частиц уноса  , где
, где  <0.
<0.
 мкм.
мкм.
Среднее квадратичное отклонение в законе распределения частиц по размерам:
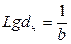 , где
, где 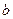 >0.
>0.
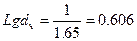
Для изображения прямой  на графике в области существования данных зададимся двумя значениями аргумента и вычислим значение Х.
на графике в области существования данных зададимся двумя значениями аргумента и вычислим значение Х.
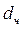 , мкм , мкм
| ||
| Х | - 0,95 | 0,20 |
Дата добавления: 2015-08-27; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОПРЕДЕЛЕНИЕ ОБЪЁМОВ ВОЗДУХА И ПРОДУКТОВ СГОРАНИЯ. | | | ВЫБОР ТИПА И РАСЧЕТ ЗОЛОУЛОВИТЕЛЯ. |