Арифметические схемы

Полусумматор (half-adder). Полусумматор предназначен для суммирования младших разрядов многоразрядных чисел.

Рис. 6 Полусумматор: а – таблица истинности;

б – реализация на вентилях; в – обозначение на схемах

Для суммирования остальных разрядов нужен полный сумматор (full-adder), который состоит из двух полусумматоров и учитывает перенос из предыдущего разряда.

Схема формирования признака переполнения строится согласно выражению:

где an–1, bn–1, sn–1 – старшие разряды слагаемых и суммы.

Рис. 7. Полный сумматор: а – таблица истинности; б – реализация на вентилях; в – обозначение на схемах

Для построения многоразрядных сумматоров нужно соединить требуемое количество полных сумматоров по каскадной схеме: выход переноса каждого сумматора связать со входом переноса следующего сумматора. Обратите внимание, что для сложения младших разрядов можно использовать полусумматор.

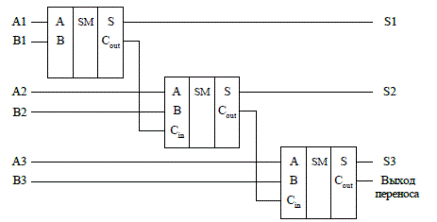
Рис. 8. Трехразрядный сумматор

Схема сдвига. Сдвиги (shifts) используются при умножении и делении.

Пример. Умножить число 1001102на 4. Разделить то же число на 2.

Решение. 1) Умножение: 1001102= 3810. 38×4=15210= 100110002.

2) Деление: 38/2 = 1910= 100112.

Те же результаты можно получить, сдвинув в первом случае двоичное число на два разряда влево, а во втором – на один разряд вправо.

Рис. 9. 4-разрядная схема сдвига

Четыре входных бита подаются на входы D0–D3. Выходные данные поступают на линии S0–S3. Линия управления С определяет направление сдвига: 0 – налево, 1 – направо.

Арифметико-логическое устройство

Арифметико- логическое устройство (АЛУ, Arithmetic Logic Unit) предназначено для выполнения арифметических и логических (НЕ, И, ИЛИ) операций.

Приведем пример одноразрядного АЛУ:

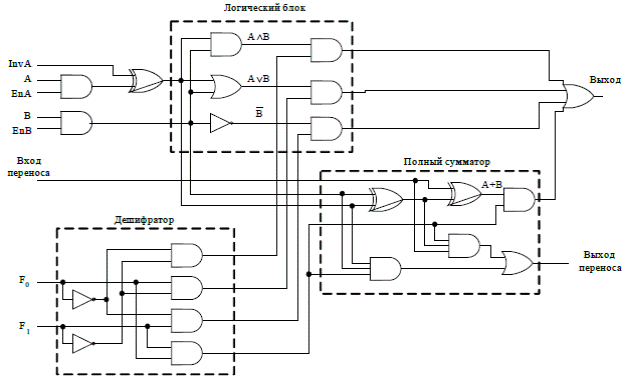
Рис. 10. Одноразрядное АЛУ

АЛУ может вычислять следующие функции: A Ù B, A Ú B, B, A+B. Выбор функции зависит от того, какие сигналы поступают на линии F0 и F1.

В левом нижнем углу схемы находится дешифратор 2х4, который выдает сигналы управления для четырех операций. Вверху схемы расположен логический блок для вычисления AND, OR, NOT. В нижнем правом углу находится полный сумматор для подсчета суммы А+В и осуществления переносов. Таким образом получается 4 выходных сигнала. Но только один из них проходит через последний вентиль ИЛИ в зависимости от того, какую из управляющих линий выбрал дешифратор. Так как ровно один из выходных сигналов дешифратора будет равен 1, то и запускаться будет ровно один из четырех вентилей И. Остальные три вентиля будут выдавать 0 независимо от значений А и В. Здесь вентили И работают в качестве ключей.

АЛУ может выполнять не только логические и арифметические операции над А и В, но и делать их равными нулю, при EnA = 0 (сигнал разрешения А) или EnB = 0 (сигнал разрешения В). Можно также получить A, установив InvA = 1 (инверсия А). При нормальных условиях EnA и EnB равны 1, а InvA = 0.

Наличие входов и выходов переноса позволяют из одноразрядных АЛУ строить АЛУ необходимой разрядности.

Тактовый генератор

Работа цифровых схем зависит от временной согласованности действий её элементов. Например, в рассмотренном АЛУ сигналы логических функций A Ù B, A Ú B, B и сигналы дешифратора должны приходить на вход вентилей И одновременно. В то же время сигналу А нужно до этого вентиля пройти три элемента, а сигналам F0, F1 – максимум два. Каждый вентиль задерживает прохождение сигнала, поэтому на вход вентиля И сигналы будут приходить не одновременно, что может вызвать ошибки в работе АЛУ. Эта проблема называется проблемой синхронизации. Она не раз ещё встретится нам в дальнейшем. Причем проблема согласованности, одновременной работы актуальна не только для вычислительных машин, но и для компьютерных сетей, операционных систем и других сложных структур.

Для обеспечения синхронизации в цифровых схемах используются тактовые генераторы.

Тактовый генератор – это схема, которая вырабатывает одинаковые по длительности импульсы через равные промежутки времени.

Формула зависимости частоты от периода:f =1/Т. Частота f кварцевых тактовых генераторов находится в пределах от 1 до 500 МГц, следовательно, период колеблется от 1000 нс до 2 нс.

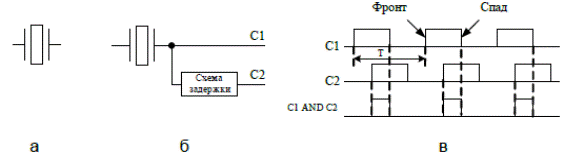
Рис. 11. Тактовый генератор: а – обозначение на схемах;

б – применение тактового генератора со схемой задержки; в – временные диаграммы

Используя схемы задержки и логические элементы, можно сформировать последовательность импульсов требуемой продолжительности и сдвига относительно основной последовательности.

Многие схемы реагируют начало или конец (фронт или спад) тактовых импульсов. На временной диаграмме (рис. 11в) показаны фронт и спад тактового импульса.

Дата добавления: 2015-08-27