Веер Кнастера — Куратовского

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Веер Кнастера — Куратовского — пример такого связного подмножества плоскости, что удаление из него одной точки делает его вполне несвязным. Предложен польскими математиками Кнастером (польск.) и Куратовским^[1]

Конструкция

Рассмотрим квадрат с центром в начале координат. На одной из строн квадрата выделим канторово множество C. Разобьём C на два подмножества A и B таких, что замыкание каждого совпадает с C (например, можно взять A и B соответственно подмножество рациональных и иррациональных точек в C). Веер Кнастера — Куратовского состоит из всех точек вида где и таких, что q рационально, если и q иррационально, если .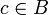

Литература

1. ↑ B. Knaster, C. Kuratowski, Sur les ensembles connexes, Fund. Math., 2 (1921) pp. 206—255.

• Александров П.С., Пасынков Б.А. Введение в теорию размерности. Введение в теорию топологических пространств и общую теорию размеренности

Дата добавления: 2015-08-27