Электродвигатели как исполнительные механизмы автоматических систем

Общие характеристики. Конструктивно электродвигательные механизмы обычно выполняются с вращательным движением выходного вала и реже с поступательным перемещением выходного штока. Однооборотные исполнительные механизмы с углом поворота выходного вала 120°...270° используются в приводе таких регулирующих органов: упоров, заслонок, кранов, шиберов. Многооборотные электродвигательные механизмы применяются для привода запорных вентилей, дросселей, задвижек, перекладчиков, сбрасывателей. Выходной вал, кроме вращательного, при помощи устройства гайка-винт может обеспечить поступательное движение, например, для привода сбрасывателя. У постоянно вращающихся исполнительных механизмов

крутящий момент от вала электродвигателя к регулирующему органу передается через электромагнитные муфты, редукторы и другие преобразователи.

Мощность электродвигательного исполнительного механизма, необходимая для перемещения нагрузки с требуемой скоростью и ускорением, определяется формулой

(4.3)

где Ν _ДВ— требуемая мощность; М _CT— статический момент, определяемый трением и несбалансированностью нагрузки; I_н — момент инерции нагрузки, включая момент инерции редуктора; I_ДВ — момент инерции электродвигателя; i _p — передаточное отношение редуктора; η — КПД редуктора; ω_Η — угловая скорость вращения нагрузки; ω_Η — угловое ускорение нагрузки.

Неизвестными в этой формуле являются требуемая мощность Ν _ДВ, момент инерции электродвигателя I _дв и передаточное отношение редуктора i _ρ· Принимая η=1, из формулы (4.3) можно получить выражение для требуемого момента на валу электродвигателя Μ _т:

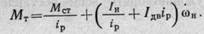
(4.4)

Найдем передаточное отношение редуктора i _{Ρ. О}, при котором требуется минимальный момент на валу электродвигателя для получения заданного ускорения нагрузки. Для этого продифференцируем выражение (1.4) по i _{Ρ. О} и результат приравняем нулю.

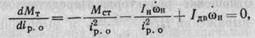
откуда оптимальное передаточное отношение

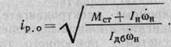
(4.5)

Подставляя выражение i _{Ρ. О} из формулы (4.5) в формулу (4.3), получим

(4.6)

По каталогу выбирается электродвигатель, мощность которого равна или несколько больше N_дв. Зная I _дв из паспортных данных двигателя, можно по формуле (4.5) определить требуемое передаточное отношение редуктора i _{Ρ. О}.

Однако выбранный электродвигатель, удовлетворяющий требованиям по мощности, может не удовлетворять требованиям по ускорению или скорости. Из формулы (4.4) видно, что ускоре-

ние перемещения нагрузки и М _T при выбранном i_p однозначно связаны, поэтому проверку необходимо провести по моменту и скорости.

Полагая, что мощность выбранного электродвигателя равна требуемой мощности, можно записать равенство

М _{дв. ном}ω_{дв. ном} = М _тω_{н. max} i _{Ρ. О}, (4.7)

где М _{дв. ном} — номинальный момент электродвигателя из паспортных данных; ω_{дв. ном} — номинальная скорость; ω_{н. max}—максимальная скорость нагрузки.

При этом возможны два случая.

1-й случай:

М _{дв. ном} ≤ М _т И ω_{дв. ном} ≥ω_{н. max} i _{Ρ. О}·

Известно, что у современных электродвигателей постоянного тока с нагрузкой пусковой момент М _пуск достигает 10 М _{дв. ном}, а у электродвигателей переменного тока М _пуск = 3 М _{дв. ном}. Поэтому, если при проверке получим, что для электродвигателя постоянного тока М _пус=10 М _{дв. ном} >Μ_τ и для электродвигателя переменного тока Ai_nycK = 3 Λί_ΑΒ. ном> М _т, то такие электродвигатели будут удовлетворять всем поставленным требованиям.

2-й случай:

М _{дв. ном} > М _т И ω_{дв. ном} <ω_{н. max} i _{Ρ. О}

В этом случае выбранный электродвигатель не сможет обеспечить необходимую скорость вращения нагрузки ω_{н. max} и поэтому необходимо выбрать другой электродвигатель и изменить передаточное отношение редуктора. Передаточное отношение

находится из выражения i _р1 = ω_{дв. ном.}/ω_{н. max} и выбранный электро-

двигатель с измененным передаточным отношением редуктора будет обеспечивать заданную скорость.

Двухфазные асинхронные электродвигатели. Двухфазные асинхронные электродвигатели нашли применение в АСР и маломощных следящих системах приборного типа. Они входят в комплект некоторых автоматических потенциометров и мостов, бытовой техники.

На статоре (рис. 4.2, а) располагается управляющая обмотка W ₁ и обмотка возбуждения W₂· Электрические оси обмоток в пространстве смещены на 90°. К обмотке W₁ подводится напряжение от выходного элемента регулирующего устройства. Обмотка W₂ питается напряжением U _В от сети через емкость С, которая служит для сдвига фазы напряжения на этой обмотке на 90 эл. градусов.

Все это создает вращающееся электромагнитное поле статора, индуцирующее токи в роторе, который представляет собой

алюминиевый цилиндр. Взаимодействие поля статора с токами ротора создает вращающий момент. Как видно из рис. 4.2, б, скорость вращения и вращающий момент увеличиваются с увеличением управляющего напряжения U_y.

Динамика двухфазного асинхронного электродвигателя описывается дифференциальным уравнением в операторной форме:

[ T _М Т _Э Р ² + (Т _м + Т_э) Ρ + 1] ω = kU_y, (4.8)

где T _М= I _дв k ₁ — электромеханическая постоянная времени; I _дв— момент инерции ротора; k и k₁ — коэффициенты, зависящие от

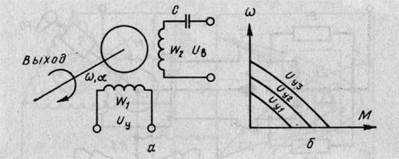
Рис. 4.2. Схема и механическая характеристика двухфазного асинхронного

электродвигателя

характеристик двигателя; Т_э=L/R - электрическая постоянная

времени обмотки управления; L и R — индуктивность и активное сопротивление обмотки управления.

В следящих системах регулируемой величиной является угол поворота α ротора двигателя.

Учитывая, что ω = d α/ dt или в оперативной форме ω = Ρα, из

выражения (4.8) получим уравнение динамики относительно угла поворота:

[Т_МТ_ЭР³ + (Т_М + Т_Э) Р² + Р] α = kU_y. (4.9)

В установившихся режимах работы формулы (4.8), (4.9) определяют соответственно характеристики электродвигателя:

ω = kU_y; α = kU_yt.

Однооборотные исполнительные механизмы (ИМ). На базе двухфазных, трехфазных, асинхронных электродвигателей строится широкий класс однооборотных исполнительных механизмов типа МЭО на 220 В, на 380 В и др. Используются они для привода задвижек, заслонок, шиберов, сбрасывателей. В частности,

исполнительный механизм МЭО (рис. 4.3) представляет собой асинхронный двухфазный электродвигатель М, который через редуктор Ρ приводит во вращение регулирующий орган РО кривошипного типа, воздействующий на объект управления. На противоположном валу ротора установлен кулачок К, воздействующий при крайних положениях регулирующего органа на концевые выключатели S2, S3, отключая двигатель М. Показывающий и сигнализирующий прибор ПС_Г указывает положение регулирующего органа РО. Прибор ПС_Г включен с потенциометром R3, движок которого кинематически связан с ротором

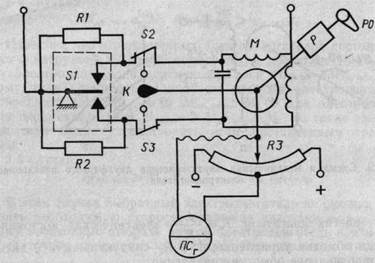
Рис. 4.3. Однооборотный исполнительный механизм

двигателя М. Величина угла поворота, при котором срабатывают конечные выключатели S2, S3, задается соответствующей установкой кулачка К. Включение, реверсирование и отключение двигателя Μ осуществляется ключом S1 автоматического или ручного устройства управления. Сопротивления R1, R2 уменьшают выбег двигателя при его остановке.

Основными характеристиками однооборотных электродвигательных исполнительных механизмов является необходимый максимальный момент M_max на валу регулирующего органа РО и время полного поворота Т_в вала РО.

Мощность двигателя N _дв, соответственно и тип ИМ выбирается по формуле

(4.10) где η — КПД редуктора.

Асинхронные трехфазные электродвигатели переменного тока с короткозамкнутым ротором. Широко применяются в качестве постоянно вращающихся исполнительных механизмов. Обмотки статора соединены обычно или звездой или треугольником (рис. 4.4, а).

Уравнение вращения ротора трехфазного электродвигателя

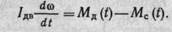
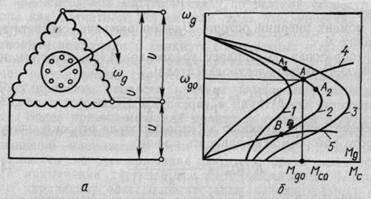
Рис. 4.4. Схема и механические характеристики асинхронного трехфазного электродвигателя с короткозамкнутым ротором

напряжения питания U, угловой скорости ротора ω (см. кривые 1 — 3 на рис. 4.4, б), т. е.

М_д(t) = М_д(ω, U). (4.12)

Момент сопротивления М_с изменяется по кривой 4 (рис. 4.4, б)

М_с(t) = М_с(ω). (4.13)

Учитывая нелинейность характеристик М _д и М _с, линеаризуем их в малом диапазоне изменения угловой скорости Δω (между точками А ₁ и А₂). В точке А при ω_до имеем установившееся значение

М _ДО =М _СО. (4.14)

Разлагая характеристики М_Д и М_С в окрестностях точки А в ряд Тейлора, используя по два члена разложения из линейной

части и подставив полученные выражения в уравнение (4.11) с учетом соотношения (4.14), получим

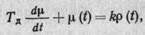
(4.15)

Где

I _дв —момент инерции ротора; U_o — напряжение, соответствующее точке А.

Преобразовав по Лапласу уравнение (4.15), получим передаточную функцию электродвигателя:

(4.16)

Передаточную функцию электродвигателя относительно угла поворота ротора можно записать в виде

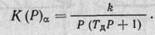
В выбранной точке А рабочего диапазона двигателя наклон характеристики(∂M_С/∂ω) больше наклона характеристики (∂M_Д/∂ω),

поэтому передаточные функции (4.16) и (4.17) являются устойчивыми. В диапазоне неустойчивой характеристики для точки В (∂M_С/∂ω)<(∂M_Д/∂ω) и соответствующие передаточные функции будут неустойчивыми

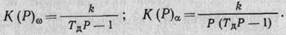
Скорость вращения асинхронного электродвигателя определяется формулой

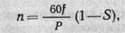
(4.18)

где f — частота тока, Гц; S — скольжение, Ρ — число пар полюсов. Поэтому для изменения скорости вращения ротора необходимо изменять эти параметры.

Частотное регулирование позволяет в широком диапазоне изменять скорость вращения, для чего используются тиристор-ные преобразователи. Исполнительные механизмы с частотным

управлением находят применение в разомкнутых системах регулирования скорости. Механические характеристики привода с частотным управлением жесткие.

Кроме того, в практике используется частотно-токовое управление, независимым параметром является амплитуда тока, питающего электродвигатель. В общем случае амплитуда тока электродвигателя формируется при помощи двух входных сигналов: для управления моментом, для управления магнитным потоком электродвигателя. Частота изменения токов электродвигателя при частотно-токовом управлении в отличие от частотного не является независимым параметром, а образуется за счет положительной обратной связи по угловой скорости, или ротора как магнитного потока, или ЭДС. Механические характеристики здесь мягкие. Поэтому частотно-токовое управление в основном применяют в замкнутых скоростных и позиционных системах регулирования, а также применяют в разомкнутых системах регулирования скорости нагрузок вентиляторного типа.

Регулирование скорости прямым изменением скольжения возможно в небольшом диапазоне и практически применяется редко. Более приемлемым для практики является регулирование скорости двигателя изменением напряжения в сети. При уменьшении напряжения сети увеличивается скольжение и уменьшается скорость вращения двигателя. Здесь также эффективно применение тиристорных преобразователей. Такие системы управления электродвигательных исполнительных механизмов применяются как в разомкнутых, так и в замкнутых АСР скорости.

На принципе изменения числа пар полюсов выпускаются 2— 4—8-скоростные асинхронные электродвигатели.

Электрические исполнительные механизмы с электродвигателями постоянного тока. Электродвигатель постоянного тока имеет преимущества перед другими типами электроприводов по величине диапазона плавного регулирования скорости и больших пусковых моментах. Особенно целесообразно использовать эти электродвигатели для объектов, где нагрузка имеет ударный или толчкообразный характер и где необходим широкий диапазон плавного регулирования скорости. Двигатели имеют достаточно высокое быстродействие, высокий КПД. Это и обусловило широкое применение электродвигателей постоянного тока с комплектными тиристорными преобразователями в системах регулирования подачи шпалорезных установок, лесопильных рам, деревообрабатывающих станков.

Электродвигатели постоянного тока классифицируются на двигатели с электромагнитным возбуждением и с возбуждением от постоянных магнитов.

Двигатели с электромагнитным возбуждением подразделяются на электродвигатели с независимым, последовательным,

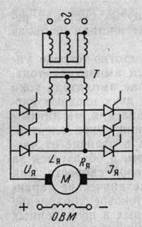
Рис. 4.5. Схема электродвигателя постоянного тока с тиристорным преобразователем

параллельным и смешанным возбуждением.

Скоростная характеристика электродвигателя постоянного тока определяется уравнением (4.19)

(4.19)

где n — частота вращения; U — приложенное напряжение, В; I _я — ток цепи якоря, А; Ф — магнитный поток возбуждения; R_я — сопротивление цепи якоря, Ом; k — коэффициент, зависящий от конструктивных параметров двигателя.

Уравнение (4.19) указывает на три возможных способа регулирования скорости вращения электродвигателя изменением: сопротивления в цепи якоря, приложенного напряжения и потока возбуждения. Практическое применение нашли два последних способа регулирования. Для этих способов применяют управление якорным напряжением, возбуждением или с одновременным управлением возбуждением и напряжением, подводимым к якорю двигателя.

Наибольшее распространение получил способ управления напряжением, подводимым к якорю. Этот способ дает возможность получить достаточно широкий диапазон изменения частоты вращения, плавность регулирования. Наиболее современным принципом управления электродвигателем постоянного тока являются схемы с тиристорными преобразователями (рис. 4.5). Регулирование угловой скорости двигателя вверх до основной (при полностью открытых тиристорах) и регулирование вниз — изменением угла включения тиристоров при неизменном потоке возбуждения.

Уравнения семейства механических ω (Μ_Д) и скоростных ω(U_Я) характеристик распространенного электродвигателя постоянного тока с независимым возбуждением имеют вид

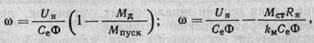
(4.20)

где ω — угловая скорость вращения якоря; Μ_Д — вращающий момент на валу электродвигателя; U_Я — напряжение, приложенное к якорю, В; R_Я — сопротивление якоря, Ом; Μ_ПУСК — пусковой момент; М_ст — статический момент нагрузки; С_е — коэф-

фициент противо-ЭДС; k_M — коэффициент вращающего момента.

Из формул (4.20) нетрудно сделать оценку механических и скоростных свойств двигателя.

Динамика электродвигателя постоянного тока с независимым возбуждением описывается следующим дифференциальным уравнением в операторной форме:

[ Т _м Т _э Р ² + Т _м Р + 1]ω = kU _я (4.21)

или относительно угла поворота якоря а, с учетом ω = d

получим

[ Т _м Т _э Р³ + Т _м Р ² + Р ]α = kU _я,

где Т _м— электромеханическая постоянная времени; Т _м =

= I _двω₀/Μ_ПУСК; I _дв — момент инерции; ω₀ — угловая скорость иде-

ального холостого хода; -Μ_ПУСК — пусковой момент; Т_э — электрическая постоянная времени; Т_э= L_Я/R_Я; L_Я и R_Я — индуктив-

ность и активное сопротивление цепи якоря; k — коэффициент, определяемый скоростной характеристикой электродвигателя.

Дата добавления: 2015-08-27