
|
Читайте также: |
Найти общее или частное решение (если даны начальные условия) решение дифференциального уравнения:
5.1.  .
.
5.2.  .
.
5.3.  .
. 
5.4.  .
.
5.5.  .
.
5.6. 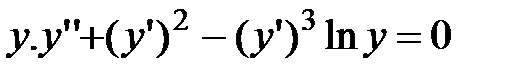
5.7. 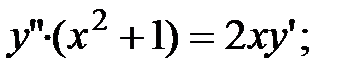
 ,
, 
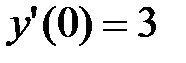 .
.
5.8. 
 ,
, 
 .
.
5.9. 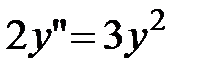 ;
; 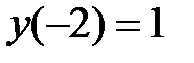 ,
, 
5.10.  .
.
5.11. 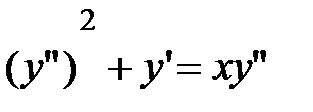 .
.
5.12. 
 .
.
5.13. 
5.14. 
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 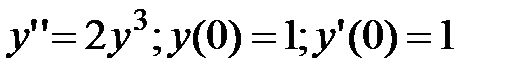
Ответы:
5.1. 
5.2. 
5.3. 
5.4. 

5.5.  (или
(или  ).
).
5.6. 

5.7. 
5.8. 
5.9. 
5.10. 
5.11. 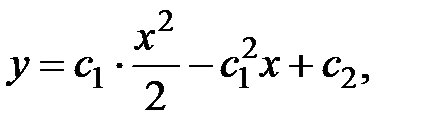

5.12. 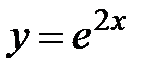
5.13. 
5.14. 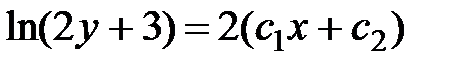
5.15. 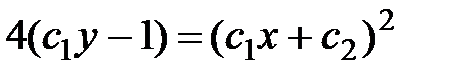
5.16. 
5.17. 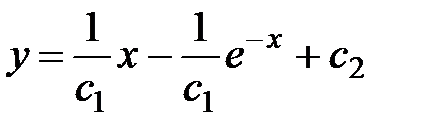
5.18. 
5.19. 
5.20. 
З а м е ч а н и е. Дифференциальные уравнения вида  не содержащие в явном виде как независимой переменной x, так и искомой функции y, можно решать как ДУ вида (2), с его частными случаями, так и вида (3), но вид (3) проще.
не содержащие в явном виде как независимой переменной x, так и искомой функции y, можно решать как ДУ вида (2), с его частными случаями, так и вида (3), но вид (3) проще.
Таблица 1.
Типология ДУ второго порядка, допускающие понижение порядка
| Характерные признаки | ДУ второго порядка, способ его решения |
| 1. В левой части ДУ содержится только производная, в правой части – функция f(x). |
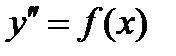 -простейшее
· интегрировать обе части ДУ, в результате получится ДУ -простейшее
· интегрировать обе части ДУ, в результате получится ДУ
 ;
· решить полученное ДУ 1-го порядка путем интегрирования, найти общее решение ;
· решить полученное ДУ 1-го порядка путем интегрирования, найти общее решение
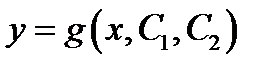 или общий интеграл. или общий интеграл.
|
| 2. ДУ не содержит в явном виде функцию y |  · замена
· замена  приводит к ДУ 1-го порядка;
· решить полученное ДУ 1-го порядка, найти приводит к ДУ 1-го порядка;
· решить полученное ДУ 1-го порядка, найти  ;
· обратная замена ;
· обратная замена  в найденное решение приводит к простейшему ДУ 1-го порядка;
· решить полученное ДУ 1-го порядка, найти в найденное решение приводит к простейшему ДУ 1-го порядка;
· решить полученное ДУ 1-го порядка, найти 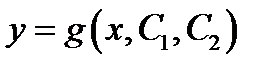 . .
|
| 3. ДУ не содержит в явном виде x |  .
· замена .
· замена  приводит к ДУ 1-го порядка относительно p;
· решить полученное ДУ 1-го порядка, найти общее решение приводит к ДУ 1-го порядка относительно p;
· решить полученное ДУ 1-го порядка, найти общее решение  или общий интеграл;
· обратная замена или общий интеграл;
· обратная замена 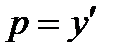 в найденное решение приводит к ДУ 1-го порядка;
· решить полученное ДУ, найти общее решение в найденное решение приводит к ДУ 1-го порядка;
· решить полученное ДУ, найти общее решение  или общий интеграл. или общий интеграл.
|
Дата добавления: 2015-08-26; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 4.Найти частное решение ДУ | | | ИСТОРИЯ ДЕРМАТОВЕНЕРОЛОГИИ |