Пример 2.Найти общее решение ДУ

Решение:

· Замена , приводит к ДУ первого порядка:

.

Это однородное ДУ.

· Решим полученное ДУ, полагая

Подставим в уравнение, получим

Интегрируя почленно, находим

Обратная замена дает общее решение ДУ первого порядка относительно z:

· Обратная замена в найденное решение z вновь приводит к простейшему ДУ первого порядка

· Интегрируя по частям, найдем общее решение:

Ответ:

5.3. Дифференциальные уравнения 2- го порядка не содержащие в явном виде независимой переменной x.

Способ решения ДУ вида:

(3)

состоит в понижении порядка на единицу с помощью замены . В этом случае за независимую переменную примем y. Тогда y=y(x) - искомая функция. При этом 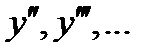находятся по формулам дифференцирования сложной функции и произведения функций:

Для решения ДУ такого вида рекомендуется следующий порядок действий.

· Понижается порядок ДУ на единицу с помощью замены: которая приводит его к ДУ первого порядка .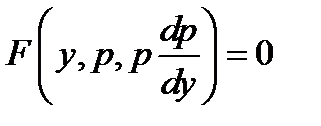

· Решается полученное ДУ первого порядка относительно p.

· Обратная замена в найденное решение приводит вновь к ДУ первого порядка.

· Решается полученное ДУ первого порядка, находится общее решение или общий интеграл.

Дата добавления: 2015-08-26